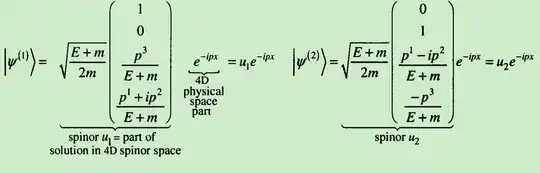Why do we say that photons have spin 1 comparing with the fermoins?

Question

I am learning QFT， and I find it very difficult to understand the spin of photon. Firstly I have some facts listed here:

1. We can get the spin of an electron from Dirac equation. The reasons for electrons to have two spin polarizations are due to: The dimension of the physical space time is 4 Why don't we construct a spin 1/4 spinor?. Therefore, if we want to construct a spin space, we need at least four bases vectors. For fermions, we can use two complex bases vectors to construct a spinner(hence two spin polarization states) . This is because, these two could provide four independent variables since complex. This can be easily seen from below:

The word spin comes from the fact that when we try to make a link or map between the spin space and the real physical space, we need, locally, the Lie algrebra, which is responsible for the spinning behaver: SU(2)~SO(3) locally.

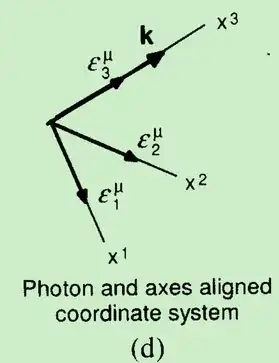
2.For photons, things are much the same. However photon polarization expands a 4 dimensional real space! Therefore 4 bases vectors are needed. And hence, it has four polarizations. But, different from fermions, when we map this polarization space with the real physical space, we do not need locally Lie algebras! see below, we can simply align their bases:

My question is :

Since we don't have to use Lie algebra for photons why do we have photon spin? I know that only two polarizations are physical, but how are the other, especially linear polarization case, related to spinning without mathematical structures like Lie algebra?

I also know from student friendly QFT that circular polarization is not spin, so if any answers that say the linear polarization can be treated as the superposition of circular cases, would you please explain more?

following is from student friendly QFT

Answer 1

Finally, I find the answer that I want.

The question is not very well asked!

There are four things, which need to be stated:

1.A polarization space. For fermions it is the spin space and for photons it is the polarization space.

2.A rotation plane in the polarization space. For electrons it is the $u_1\times u_2$ plane, for positrons it is the $v_1\times v_2$ plane and for photons it is the $\epsilon _1^{\mu }\times \epsilon _2^{\mu }$ plane (we should have actually $C_4^2$ many planes since we have four polarizations, while however, two polarizations are not physical).

3.The map of the polarization space onto real 4-d physical. For electrons, the rotation in spin space by angle $\theta$ in the $u_1\times u_2$ plane corresponds to a rotation of angle $2 \theta$ in the real physical space about a certain definite axis (the static case). This is due to the fact that we cannot align the spin space with the real physical space. For photons, the rotation in polarization space by angle $\theta$ in the $\epsilon _1^{\mu }\times \epsilon _2^{\mu }$ plane corresponds to a rotation of angle $ \theta$ in the real physical space about a certain definite axis . This is due to the fact that we can indeed align the spin space with the real physical space.

4.Hence, the number of planes in the polarization space determine the possible types of spins (for example spin 1-half is one type, and spin 1 is one type). But the map between polarization space and real space determine the spin values(for instance 1 or 1-half ?) of each possible type.