7

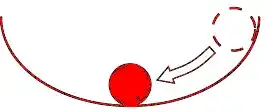
I do understand that in the case of mechanics for example, if there is a soccer ball inside a "well", at mechanical equilibrium, the ball will be at the bottom of the well.

ball
(source: utk.edu)

This is a consequence, of the fact that the potential has a minimum there. By definition, the force (derived from this potential) acting on the ball will make the ball go at the bottom for small fluctuations around equilibrium position.

But in the case of $E(S,V,N)$, I don't see where is the "force" that will keep E at the minimum for small fluctuations of $S,V$ and $N$.

Actually, the following section of my course does the following to define equilibrium:

$$\frac{\partial E}{\partial S} =T$$

$$\frac{\partial E}{\partial V} =0$$

$$\frac{\partial E}{\partial N} =0$$

Thank you for reading.

Community
  • 1
Pao
  • 233

1 Answers1

1

Because there exists a minimum in energy, the free energy is locally convex at that point. The existence of a minimum in the energy, given fixed entropy S, is equivalent to the entropy maximisation principle: https://en.wikipedia.org/wiki/Principle_of_minimum_energy

Convexity is commonly talked about as the property that tells you you are in a stable regime , away from a phase transition. If you have 2 separate minima of the free energy, separated by a concave 'hill', then each minima is a distinct stable 'phase'. The system is then either found completely in either of the two phases, or the free energy function is linearized in the concave region in which case you are in a phase transition.

Aritro Pathak
  • 741