Why is the $B$-Field an axial Vector?

Question

in trying to understand the Wu-Experiment I wonder why the $B$-Field is an axial vector. I know that $\vec{B} = \vec{\nabla} \times \vec{A}$. Under Parity transformation I'd expect $\vec{A} \rightarrow -\vec{A}$, however I don't know whether $\vec{\nabla} \rightarrow -\vec{\nabla}$.

Answer 1

Maybe the best way is to think about $\vec{B}$ in terms of the Biot-Savart law.

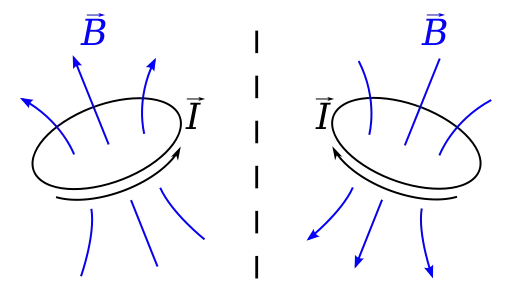
Imagine a loop carrying a current $I$ in a plane that is perpendicular to a mirror. The Biot-Savart law says that the B-field at position $\vec{r}$ is given by $$\vec{B}(\vec{r}) = \frac{\mu_0}{4\pi}\, \oint \frac{I\, d\vec{l} \times \vec{r'}}{|\vec{r'}|^2}\ dl, $$ where $\vec{r'} = \vec{r}-\vec{l}$ is the displacement from an element on the loop to where the field is calculated.

This is an axial vector because if we look at this situation in a mirror, the current would appear to flow in the opposite sense, $\vec{l}$ is reversed and the $\vec{B}$ field should actually be in the opposite direction to its mirror image. i.e. An actual mirror image would look like it was obeying a left-hand rule, rather than a right-hand rule.

This is actually exactly the example used on the wikipedia page on pseudovectors, which is another name for an axial vector.

In this example, both $\vec{l}$ and $\vec{r}$ are displacements and are true vectors. Their vector product must be an axial vector.

You are asking about a parity transformation, but as far as I am aware $\vec{B}$ is unchanged by a parity inversion. Axial vectors do not change signs under parity inversions. Angular momentum is another example of an axial vector that does not change under a parity inversion. $\vec{A}$ on the other hand is a true vector and has its sign flipped by a parity inversion. The curl of a true vector is an axial vector and the curl of an axial vector is a true vector. So $\nabla$ is behaving as a true vector in this regard where $\nabla \rightarrow -\nabla$ is odd under a parity inversion (because $\partial/\partial x \rightarrow -\partial/\partial x$ etc.)

Answer 2

(Within Netwonian mechanics) You can start with Lorentz Force law $$\vec{F}=q\vec{E}+q\vec{v}\times\vec{B}$$We know that $\vec{F}$ is a physical vector(From Newton's law). We also know that $\vec{v}$ is a physical vector. Therefore $\vec{B}$ must be an axial vector.