I have asked this question in the math SE but no one there knew an answer; there are similar questions here but they differ a bit from what I am trying to understand.
I was wondering if there is an (analytical) solution to the problem (in 2D) where the position $\vec{r}_i = \vec{r}(t=t_i)$, $\vec{r}_f = \vec{r}(t=t_f)$ and the velocities $\vec{v}_i = \vec{v}(t=t_i)$, $\vec{v}_f = \vec{v}(t=t_f)$ as well as the constant magnitude of acceleration $|a|$ are given and the goal is to find the vector $\vec{a}(t)/|a| = \vec{e}_a(t)$ that minimizes the time need to transition from the initial state to the final state assuming there are no other forces present.
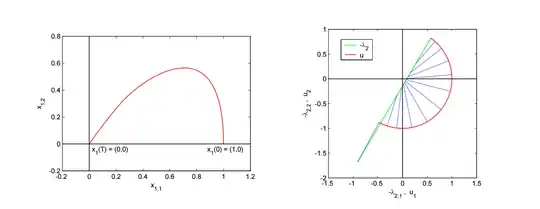
There is this paper I found that explains the solution based on it's geometric properties. On page 5 there is a graph that shows that the acceleration is a semicircle rotated and offset from the center with the radius $|a|$ but I don't understand exactly how to compute the actual values for a given initial and final state.
I know about Lagrangian multipliers and after reading the Wikipedia page I understand the shooting method but I don't know much about optimal control boundary value problems in general so and extended answer would be appreciated. Thanks in advance for your answers!