What is the exact shape of the universe? I know of the balloon analogy, and the bread with raisins in it. These clarify some points, like how the universe can have no centre, and how it can expand equally everywhere in all directions.
But they also raise some questions, like if you are on the surface of a balloon and travel in 1 direction, you will eventually return to your starting point, is it possible our universe have this feature?
If it has, or had, would this be a symmetry of sorts ($\psi(x)=\psi(x+R)$), and as such have a conserved quantity associated with it (by Noether)?
Assuming "small curled up dimensions" wouldn't these dimensions have this type of symmetry, what are the associated conserved quantities?
Is it known exactly what the geometrical shape of the universe is? (on a large scale) (I am not talking about only the observable universe).
How does one define the "size" of a dimension, is this scale only applicable to curled up ones?
Is it possible to describe to a layman the shape of the universe without resorting to inept analogies?
- 220,844
- 5,341
5 Answers
There are a bunch of questions here. Let me try to take them in order:
- Is it possible that our Universe has the feature that if you travel far enough you return to where you started?
Yes. The standard Big-Bang cosmological model is based on the idea that the Universe is homogeneous and isotropic. One sort of homogeneous spacetime has the geometry of a 3-sphere (like a regular sphere, but with one more dimension). In these cosmological models, if you travel far enough you get back to where you started.
However, the best available data seem to indicate that the Universe is very nearly spatially flat. This means that, if we do live in a 3-sphere Universe, the radius of the sphere is very large, and the distance you'd have to travel is much larger than the size of the observable Universe. Even if that weren't true, the fact that the Universe is expanding would make it hard or impossible to circumnavigate the Universe in practice: no matter how fast you went (short of the speed of light), you might never make it all the way around. Nonetheless, 3-sphere Universes, with the geometrical property you describe, are definitely viable cosmological models.
- Does this give rise to a symmetry by Noether's theorem?
Not really. Noether's theorem is generally applied to continuous symmetries (i.e., ones that can be applied infinitesimally), not discrete symmetries like this. The fact that space is homogeneous gives rise to a symmetry, namely momentum conservation, whether or not space has the 3-sphere geometry, but the symmetry you're talking about here doesn't give rise to anything extra.
- Would small curled up dimensions have the same sort of symmetry?
I'll leave this for someone else, I think. Not my thing.
- Is it known exactly what the geomtrical shape of the universe is?
No, and don't let anyone tell you otherwise! Sometimes, especially in pop-science writing, people imply that we know a lot more about the global properties of the Universe than we do. We often assume things like homogeneity to make our lives simpler, but in fact we have precisely no idea what things are like outside of our horizon volume.
- How to describe the "size" of a dimension?
If the Universe's geometry has enough symmetries, it makes sense to define an overall time coordinate everywhere. Then it makes sense to imagine a "slice" through spacetime that represents the Universe at an instant of time. If some of those slices have the geometrical property you're talking about, that traveling a distance R in a certain direction gets you back to your starting point, then it makes sense to call R the "size" of the corresponding dimension. If you can travel forever, then we say the size in that dimension is infinite.
- Is it possible to describe to a layman the shape of the universe without resorting to inept analogies?
All analogies are imperfect. I think the best you can do is use a bunch of them and try to convey the limitations of each.
- 20,263
the answer to the Magellan question for our Universe is actually "No". If the Universe were a static 3-sphere, as Ted Bunn suggests, then you could "swim" around the Universe just like Megallan around the Earth.
But an important fact about our Universe is that its size is changing: the size can't stay constant just like the apple can't sit in the middle of a bedroom (in the air) - that's another thing that gravity according to general relativity guarantees. Already today, it resembles an empty de Sitter space (because the dark energy or cosmological constant is the majority of the energy in the Universe) that is exponentially expanding. The so-called Penrose causal diagram of the de Sitter space

shows that there are no time-like (mostly vertical) trajectories in it that would lead you to the same place, given by the $x$ coordinate. That's because the height of the diagram (square) is so limited.
So it will never be possible to travel along a straight line, even if you approached the speed of light, and return to the same place where you started (and meet your civilization that didn't travel anywhere). The time-dependence of the size of the Universe is important for this conclusion.
The spatial section of our Universe is nearly flat - that's because the total density (including dark energy and dark matter) is very close to the critical density, a fact guaranteed by the cosmic inflation. It may be slightly positively curved, like a 3-sphere (the surface of a 4-dimensional ball), or slightly negative curved (the surface of a hyperboloids resembling a saddle, but 3-dimensional one).
The whole spacetime geometry is close to the 4-dimensional de Sitter space that may be written as the following hyperboloid in 4+1 dimensions: $$ -A^2+B^2+C^2+D^2+E^2=R^2 $$ where $R$ is the radius of the curvature.
Concerning another question you asked: if the Universe is compact, like a sphere, then the wave function may be simply thought of as a wave function of the sphere. Of course, if the sphere is parameterized by some coordinates such as the latitude and longitude, it is a periodic function at least of the latter.
A sphere has a full rotational symmetry, $SU(2)$. Extra dimensions in string/M-theory can't have any continuous symmetries. They're believed to be Calabi-Yau manifolds or very similar manifolds in which all the dimensions are knitted in a nontrivial way.
If you have a compact dimension of space and you write a wave function so that it satisfies $\psi(x) = \psi(x+2\pi R)$, then indeed, it is possible to interpret this periodicity as a symmetry with respect to the (discrete) group of translations by multiples of $2\pi R$. While Noether's theorem is normally designed for continuous symmetries, you may say what the symmetry implies for such discrete symmetries as well.
The multiplicative generator of the symmetry is the translation by $2\pi R$ and it commutes with the Hamiltonian - because it is the indentity, after all. The generator may be written as $\exp(2\pi i R p)$ where $p$ is the momentum in the circular direction. And because it is equal to one, it means that the momentum is quantized in units of $1/R$ which is probably not too surprising. A problem here is that the translation by $2\pi R$ is not really a "nontrivial symmetry" in this case: it is an operation that is doing nothing at all. It keeps all objects invariant, so there is no nontrivial Noether's conserved quantity associated with it.
- 19,167
- 6
- 64
- 104
- 182,599
Since only a fraction of the universe is actually observable, I am not sure if it possible to answer this question.
- 40,139
From the NASA site: "Recent measurements (c. 2001) by a number of ground-based and balloon-based experiments, including MAT/TOCO, Boomerang, Maxima, and DASI, have shown that the brightest spots are about 1 degree across. Thus the universe was known to be flat to within about 15% accuracy prior to the WMAP results. WMAP has confirmed this result with very high accuracy and precision. We now know that the universe is flat with only a 2% margin of error." The WMAP results are given here :http://lambda.gsfc.nasa.gov/product/map/current/
- 4,413
How does one define the "size" of a dimension,
One unit of length is the distance light will go in a particular unit of time. If time passed slower, the universe would look the same, except the speed of light would look faster.
Is it known exactly what the geometrical shape of the universe is?
Yes, a hypersphere. But you can picture it as the 2D surface of a sphere if you pretend that space only has two dimensions instead of 3. Then you'll get the balloon analogy.
I know of the balloon analogy
It's the perfect analogy.
But you have to remember that the surface of the balloon, which looks like a spherical shell here, is actually our 3-dimensional universe, not a 2D surface. That's why they call it a hypersphere.
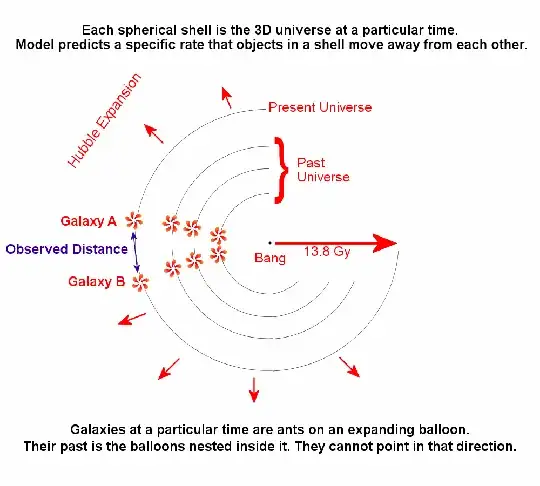
The past universe is all of the smaller balloons inside the "now" balloon. At the very center, is the Big Bang. The surface of the balloon is our universe. It is expanding into future time.
We can't point in that direction. We can only point along the surface of the balloon.
the bread with raisins in it.
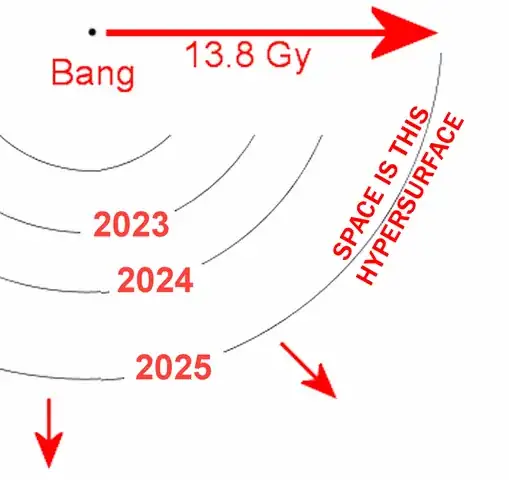
The 3D version. It's incomplete. It correctly shows the universe locally. But it totally leaves out the global geometry. It doesn't show the past. The center of the expansion is the Big Bang, but you can't see the center in that model. This is better way to look at it:
like, how the universe can have no centre,
It does, the Big Bang. Perhaps you can see why there's no time earlier than that.
and how it can expand equally everywhere in all directions.
It does that, yup. It's expanding into future time.
like, if you are on the surface of a balloon and travel in 1 direction, you will eventually return to your starting point, is it possible our universe have this feature?
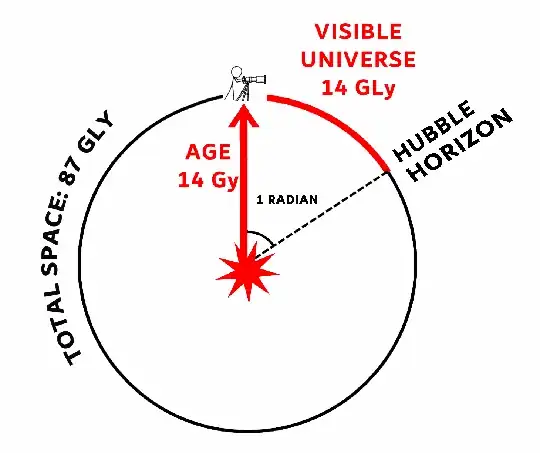
It's possible and it does, young Skywalker. The universe has been expanding for 14 billion years, which means it's total circumference around the outside is two Pi times that, 87 billion in light years.
You can validate this "expansion into time model" by noticing that, No matter what its age, the universe expands by 2Pi Light seconds per second, 1,883,652 Km — twice the distance to the moon.
=======[ Now pay attention, because this is going to look like stage magic.
What is the Megaparsec's share of that 87 billion light year universe?
The fraction is .0000376.
So what is the Megaparsec's share of the new space that is created every second?
.0000376 x 1,883,652 Km = 70.4 Km of new space every second for the Megaparsec.
=======[ That's the generally accepted value of the Hubble constant to within 1.62%
When you consider the slight uncertainties in the distances, it's correct to within 0.25%. The exact numbers are here.
Congratulations, you correctly computed the universe's expansion rate using nothing but it's age and c.
Of course, this is all just a coincidence.
Except, when the universe was very small, its surface was expanding faster than speed of light. That was inflation. The same simple arithmetic can be used to find when that ended, and the result is correct to within 10E-37 seconds.
But this isn't real because it doesn't account for dark energy.
Except it does. Dark Energy (luminosity attenuation at high Z distances) is just a consequence of the geometry, and it's just as simple as the above.
Let's see if anyone recognizes the significance of this this.
No way! I'm just a crazy nobody, therefore the numbers must not add up. I must have made an arithmetic error! One multiplication and two divisions. Yeah, that's it.