AKLT state and Nobel physics prize 2016

Question

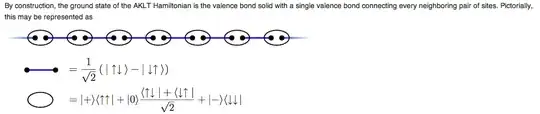
The AKLT Hamiltonian and the chain is described in Wikipedia, and also the page 17 of this year Nobel Prize advanced information

I have questions concerning the info released by nobelprize.org, and wonder whether they make some incorrect statement in my question 2 below.

The Hamiltonian is given by $$ \hat H = \sum_j \left(\frac{1}{2}\left(\vec{S}_j \cdot \vec{S}_{j+1} + \frac{1}{3} \left(\vec{S}_j \cdot \vec{S}_{j+1}\right)^2\right) + 1/3\right)=\sum_j P_2\left[\vec{S}_j + \vec{S}_{j+1}\right] $$ The version from Nobel prize info has an additional 1/2 factor and plus shifting the ground state energy by 1/3.

question 1. What is the easiest way to prove that the following spin-0 singlet pairing between the two nearest neighbor spin-1/2 states (the spin 1/2 is obtained from splitting the spin-1 on a site to two spin-1/2, defined in the oval projection below) described by the Wikipedia on AKLT is the lowest energy ground state?

question 2. I am slightly confused by the description in Nobel prize info, it says that the Hamiltonian is equivalent to the $P_2$ projector $\sum_j P_2\left[\vec{S}_j + \vec{S}_{j+1}\right]$, also it says that: "$P_2$ projects on the subspace corresponding to spin 2 on two adjacent lattice sites." What does it mean to "project to the the subspace corresponding to spin 2 on two adjacent lattice sites?" Is this statement from nobelprize.org incorrect?

Comment: My tentative thought is that if I analyze $\frac{1}{2}\left(\vec{S}_j \cdot \vec{S}_{j+1} + \frac{1}{3} \left(\vec{S}_j \cdot \vec{S}_{j+1}\right)^2\right) + 1/3$ on two neighbor sites $j$ and $j+1$, I find that the total spin-0 and the total spin-1 sectors for the two spins $\vec{S}_j + \vec{S}_{j+1}$ seems to have the lowest energy, while the total spin-2 has a higher energy, thus the total spin-2 sector has the disfavored energy penalty. Thus, shouldn't we project out the total spin-2 (get rid of the total spin-2) and project to the total spin-0 and total spin-1? Isn't that the remaining four states in the total spin-0 and total spin-1 correspond to the precise degree of freedom of the four fold degeneracy of zero modes on the open chain?

Answer 1

Question 1:
If you consider two consecutive sites in your pictures you will find that the left- and rightmost spin both have spin $\tfrac12$, while the two spins in the middle are in a singlet, i.e., have spin $0$. Together, the two sites thus have spin $$ \tfrac12\otimes 0\otimes \tfrac12 = 0\oplus 1 $$ This spin is not changed by the projection onto the spin 1 space in the AKLT construction. Thus, the two consecutive spin $1$ sites have a space $$ 1\otimes 1 = 0\oplus 1 \oplus 2\ , $$ but by the above argument the spin $2$ never shows up. Thus, a Hamiltonian which gives energy zero to nearest neighbors with spin $0$ or $1$, but positive energy for spin $2$, has this state as its ground state. As it turns out, this state is the unique ground state.

Question 2:
What does it mean to "project to the the subspace corresponding to spin 2 on two adjacent lattice sites?" Each site is a spin $1$. Two sites together thus have spin $1\otimes 1 = 0\oplus 1 \oplus 2$, i.e., we can decompose their Hilbert space as an (orthogonal) direct sum of a spin $0$, spin $1$, and spin $2$ subspace. The projector onto spin $2$ is exactly the projector onto the spin $2$ subspace.

Is this statement from Nobel prize.org incorrect? No.