I have been told that a topological defect is a discontinuity in a system that cannot be removed. Is this true? Also, can someone please explain to me what they are in more detail? And if my statement was true can someone please explain why they cannot be removed?
1 Answers
Yes, a topological defect is a discontinuity that cannot be removed.
Let me explain by giving an example similar to a liquid crystal.
Fish in a pond
I have a two-dimensional pond and I would like to fill it with fish. These fish are longer than they are wide, so when they are densely packed in the pool, they like to point in the same direction as their neighbors. Not only that, this particular species of fish like to face the same direction as their neighbors.
If I densely fill a large pond with these fish, I can define a function that describes the local orientation of the fish at any location in the pond
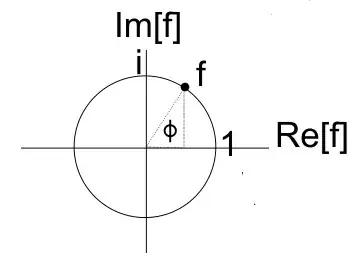
$$f(x,y) = e^{i \phi(x,y)}$$
where f is a complex number on the unit circle and is described by a real number $\phi(x,y)$ between $0$ and $2\pi$, specifying the counterclockwise angle from true east. We use this unit complex number instead of $\phi$ to make sure the continuity at $0$ and $2\pi$ is taken care of. This local orientation vector is called the director.
Here's an example of how the fish can point in different directions, $\phi$ can vary in the pool.
We'll also have the condition that the direction that our fish point changes sufficiently smoothly in the pond. This is equivalent to saying any derivatives of $f(x,y)$ are continuous, up to a sufficiently high derivative.
Now we can ask the question, what are all of the ways that our fish can fill this pond? This question is the same as asking, what are all of the sufficiently smooth unit-complex number valued functions $f(x,y)$ that can exist in our two-dimensional pool?
The answer is that it depends on the orientation of the fish at the boundary of the pool (it depends on our boundary conditions). We will see that different types of boundary conditions lead to different classes of solutions.
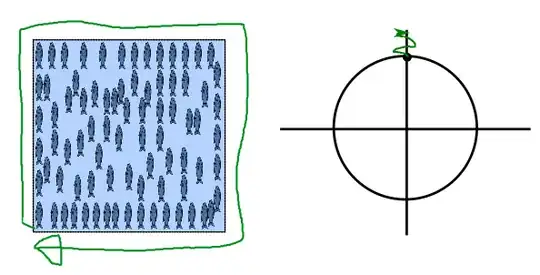
Fish at the boundary point north
Let's make all of the fish at the boundary of our pool point north.
Now, what happens when we fill the rest of the pool? There are many (infinite) solutions, but the simplest one is where all of the fish in the pool point north.
All of the fish point in the same direction, so $f(x,y)$ is constant, and there are no defects, so we'll say
$$Z=0$$
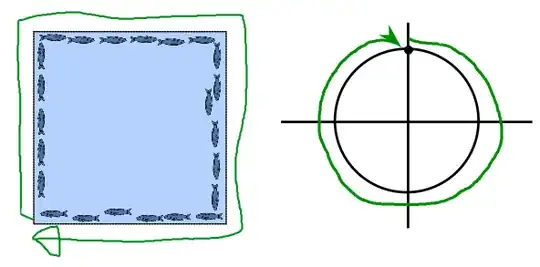
Fish at the boundary point clockwise
What happens if the fish at the boundary point in a clockwise direction?
Again, when we try to fill the rest of the pond, there are many (infinite) possible solutions. But here, the simplest solution is where all of the fish circle around the center of the pond.
Here we see our first defect. If you placed a fish at the center of the pond, it would not know which way to point! Our unit-complex valued function $f$ is not defined in the middle of the pond because of our boundary conditions.
With these boundary conditions, we are guaranteed to have one defect somewhere in the pond
$$Z=1$$
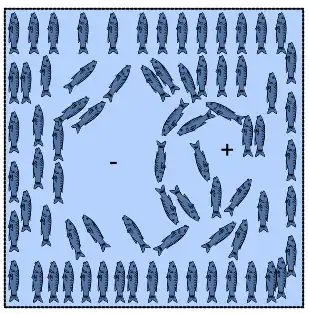
Adding and removing defects
If we take our normal $Z=0$ all fish pointing north case with no defects, we notice that we can add defects. However, if we make a region of counterclockwise fish rotation, we notice that in order to smoothly match the boundary, we must also add a different type of defect, where the direction that the fish rotate around the defect is somehow opposite of our original defect.
These two defects can be though of as 'positive' and 'negative' charges, where the net charge of zero was imposed by making all of the fish at the boundary point north.
The number of defects can be changed. But, the 'net charge' is imposed by the boundary condition, so the 'net charge' cannot be smoothly removed from a system with fixed boundary conditions.
Update
Topology is turning geometry into counting
In this case, this integer number $Z$ that characterizes the 'net charge' of the pond comes from integrating our function $f$ around the boundary
$$\int_{\text{boundary}} f(x,y) dL = \int_{\text{boundary}} e^{i\phi(x,y)} dL$$
For the $Z=0$ case where all of the fish point roughly north at the boundary, let's monitor the value of $f$ along our integral
We see that, crucially, $f$ does not wind around the unit circle during our integration. This integral is zero, and can be seen by saying that the integral picks up a positive contribution when integrating in the positive x or y direction, and an equal negative contribution when integrating in the negative x or y direction.
When the fish lie clockwise along the boundary (Z=1), our integral is different
Now, as we integrate $f$ around the boundary, $f$ does wind around the unit circle! Our integral is then
$$\int_{\text{boundary}} e^{i\phi(x,y)} dL = 1 \times (4L) = 1 \times (\text{Circumference of pond})$$
So, we've learned the possible solutions $f(x,y)$ depend on the boundary conditions, and if our function $f$ is continuous at the boundary, then all of our possible solutions fall in to different classes defined by integers Z
$$\int_{\text{boundary}} e^{i\phi(x,y)}dL = Z \times (\text{Circumference of pond})$$
where $Z$ is the number of times the fish direction winds around the circle as we integrate along the closed boundary. The fact that we can describe every possible solution $f(x,y)$ with an integer $Z$ is critical. We cannot smoothly transform a Z=0 function into a Z=1 function.
Let's try and take the Z=1 case from above, with a 'positive charge' in the middle of the pond, and smoothly move that charge out of the pond to gt all of the fish to point north.
Originally, the direction of fish along the boundary was continuous. All of the fish on the east edge pointed south. However, to move our defect out of the pond, we had to break the continuity of the direction of fish at the boundary.
Here, we just removed a topological defect from the pond. The point is that we cannot do this smoothly. At some point between Z=1 and Z=0, we had to break the continuity of the direction of the fish at the boundary. We had to change the boundary condition.