21

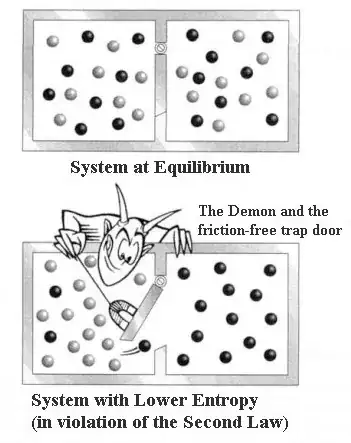
I'm trying to understand the logic behind this famous thought experiment, my confusion is as follows:

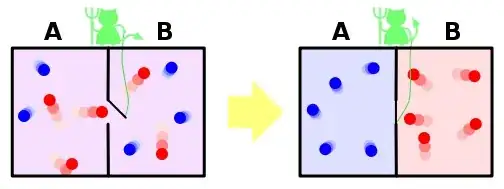
Maxwell's Demon

In the box on the right after the demon has finished his 'work', I understand that side A now has low entropy since the demon has only permitted fast-moving molecules into B. So the demon has rendered the side A full of $\color{blue}{\text{cold}}$, $\color{blue}{\text{slow}}$ moving molecules, which makes perfect sense and it seems correct to say the entropy of side A has decreased.

A quote I read recently says that

In an adiabatic expansion where the entropy stays constant the space available for the gas increases thus the speed of the molecules must correspondingly fall.

So my understanding of that statement is that the system is more disordered (entropy increases) if the space available for the gas increases, so to compensate the molecules must slow down to have $\bbox[yellow]{\text{less}}$ entropy (as the overall entropy change must be zero).

Maxwell's demon 2

According to the image above, the whole system (A and B on the right box of the previous image) has a reduced entropy.

But here's the problem: Side B is now full of $\color{red}{\text{hot}}$, $\color{red}{\text{fast}}$ moving molecules.

So does this mean that the entropy of side B has increased?

Edit:

One of the comments below (which has been deleted now) mentions that the entropy of B does increase but the overall entropy of the system (A+B) decreases.

So the question remains: why does the entropy of the system decrease and not increase?

Or put another way: why is side A more 'dominant' in the overall contribution of the system's entropy?

BLAZE
  • 2,441
  • 3
  • 35
  • 64

4 Answers4

15

You can think of entropy as measuring the amount of phase space volume that the system could be occupying. (This is the set of all possible sets of positions and momenta for all the particles.)

It's correct that the set of possible momenta are unchanged, so that doesn't affect the entropy. But the set of possible positions is lower, because it becomes correlated with momentum -- the high-momentum particles can only be in half the volume as before. That's why the entropy decreases.

You also specifically asked how the entropy of side $B$ changes. This depends on how the system is set up. If you neglect particle interactions, then side $B$ ends up with only fast particles, while it began with both fast and slow particles. Since the available phase space is lower, the entropy of side $B$ decreases.

However, if you allow particle interactions, the particles in side $B$ will reach thermal equilibrium, and you'll get a distribution of velocities (i.e. some slow, some fast, and some very fast). Then the entropy of side $B$ increases.

The first way is more common in popular presentations since it's a bit cleaner, while the second is more realistic. But in both cases, the total entropy of $A$ and $B$ decreases, which is the key point.

knzhou
  • 107,105
9

So the box is hot on the right and cold on the left. Then one can use this separation of temperature to run a heat engine by allowing the heat to flow from the hot side to the cold side. Another possible action of the demon is that he can observe the molecules and only open the door if a molecule is approaching the trap door from the right. This would result in all the molecules ending up on the left side. Again this setup can be used to run an engine. This time one could place a piston in the partition and allow the gas to flow into the piston chamber thereby pushing a rod and producing useful mechanical work.

So remembering this is a paradox, if the demon "could" do his job, a system that previously could do no work because entropy was even all over, is now able to do work, so by definition entropy has decreased.

But the demon can't do the job, so this is just assuming he could.

Using the expression for the internal energy of an ideal gas, the entropy may be written:

$${{\frac {S}{Nk}}=\ln \left[{\frac {V}{N}}\,\left({\frac {U}{{\hat {c}}_{V}kN}}\right)^{{\hat {c}}_{V}}\,{\frac {1}{\Phi }}\right]}$$

Since this is an expression for entropy in terms of $U$, $V$, and $N$, it is a fundamental equation from which all other properties of the ideal gas may be derived. Note, no explicit $T$ dependence exists, as mentioned in the comments above.

BLAZE
  • 2,441
  • 3
  • 35
  • 64
6

There are different kinds of entropy here. The thermal entropy due to the molecules moving faster or slower is a red herring and actually isn't important for understanding Maxwell's demon at all. The important entropy here is the mixing entropy that has to do with how well-sorted these different kinds of molecules are.

Personally, I think this version of Maxwell's demon shouldn't be taught in physics classes at all, even though it's the way in which Maxwell originally formulated it. A much more straightforward way of explaining Maxwell's demon is to just talk about different kinds of molecules like Nitrogen vs Oxygen. (An even simpler version is to just call them blue and red balls, although this may lead people to ask how balls tiny enough to be considered "microscopic" can have distinct colors.)

Whether blue and red, Nitrogen and Oxygen, or fast and slow, the important point is just that there are 2 different types of particles. And when they are all mixed together this is a state of high entropy, whereas when they are carefully separated into different chambers this is a state of low entropy.

reductionista
  • 1,944
3

We can imagine we have two different systems, one next to the other, we do not need to consider changes in volume. The reason being that entropy is extensive: if you have a system of volume V and separate the volume in two by adding a partition, the total entropy will not change. Also, entropy is a function of state, so it does not matter the path it takes to reach one state from another, the change in entropy will be the same regardless of the path you chose. Having said that, let us calculate the change in entropy for a partitioned system that goes from the same temperature in both sides to one that had different temperatures in both sides. For a single system the change would be:

$$\Delta S=mC\ln(T_\textrm{final}/T_\textrm{initial})$$

If we call the initial temperature $T_0$, then the total change in entropy for both systems will be:

$$\Delta S=\Delta S_1+ \Delta S_2= mC\ln\left(\frac{T_0+\Delta T}{T_0}\right)+mC\ln\left(\frac{T_0-\Delta T}{T_0}\right)= mC\ln\left(1-\left(\frac{\Delta T}{T_0}\right)^2\right)\lt 0 $$