Suppose an electric field ${\mathbf E}(x,y,z)$, $$E(x)=ax, \quad E(y)=E(z)=0,$$ where $a$ is a constant. So we can calculate its charge density is $$\rho = \varepsilon \nabla\cdot{\mathbf E} = \varepsilon a,$$ which is uniform everywhere!
But why? How could an uniform charge density create a field that point in particular direction?
First of all, your field is not uniform. You have $$ \vec E(\vec x) = \begin{pmatrix} a x \\ 0 \\ 0 \end{pmatrix} \,.$$
That looks like this:
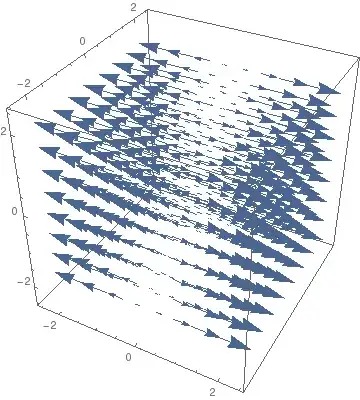
This means that for larger $x$ the field is stronger and for $x \to - \infty$ the field will be very negative.
The charge density is $\rho = \varepsilon \vec \nabla \cdot E$, which is indeed just $\varepsilon a$. This indeed looks strange as the whole information about the direction is lost. Suppose we have another electric field like this: $$ \vec E(\vec x) = \begin{pmatrix} 0 \\ ay \\ 0 \end{pmatrix} \,.$$ This would have the same charge density associated with it.
It might sound like a contradiction, but the answer is that the charge density does not uniquely specify the electric fields. This can be seen most easily by thinking about a particular charge configuration in otherwise empty space. The resulting electric field will be unique. Now put the same thing in a huge capacitor and add an extra electric field. This is not taken into account by the local charge density $\rho$ that can be obtained from the electric field.
You can always add a harmonic function (that is $\vec \nabla^2 \phi(x) = 0$) to the potential without altering the charge configuration since $\rho \propto \vec \nabla^2 \phi$. So we can go from one $\vec E$ to the other $\vec E$ by adding the field $$ \tilde{\vec E}(\vec x) = \begin{pmatrix} -ax \\ ay \\ 0 \end{pmatrix} \,.$$ The potential which generates this is defined by $\tilde{\vec E} = - \vec \nabla \cdot \tilde \phi$. This difference potential could be $$ \tilde \phi = - \frac a2 x^2 + \frac a2 y^2 \,. $$ You see that $\vec \nabla^2 \tilde \phi = 0$. Therefore this does not change the charge density but it does change the field.
In order to get a unique electric field from a charge configuration you need to specify the boundary conditions. They can be either the value of $\phi$ at some boundary of the the value of $\vec E$ (which is the derivative of $\phi$. The charge density alone does not give a unique field.
A common boundary condition is that the field goes to zero at infinity. This is what I have implied when I said the charge configuration should be in “empty space”.
