What about full moon night and what about the night without moon?
Let's say in both cases we have no clouds and +25C air.
How big should the glass be to burn the paper? ant?
2 Answers
SIGNIFICANTLY UPDATED ANSWER
TL;DR: you can get to almost 200 °C because the component of reflected sunlight adds significant power. This calculation contradicts the assertion "no hotter than the moon" - which would get you to 123°C. Big thanks to @JánLalinský who pushed me in the comments to think more deeply about this.
The best you can hope to do with an optical system is make it look like your object is completely surrounded by the thing you are imaging. If the thing you are imaging is a pure black body radiator, the temperature you can reach is the temperature of the object you are imaging. Now the moon isn't just a black body - it is also reflecting a bit of solar radiation, which complicates thing.
But as a first approximation, we can look at the surface temperature of the moon. According to this link, the surface of the moon can reach 123 C. That sets a lower limit on the temperature you can reach with an optical system that surrounds an object with lunar radiation from all sides. The reflected sunlight will add a little bit to this. We can try to estimate that.
The intensity of sunlight at the surface of the moon, compared to the intensity at the surface of the sun itself, goes as the square of the distance sun-moon divided by the radius of the sun (in effect, the light that was concentrated over the surface of the sun is now spread over a sphere that is roughly the size of the earth's orbit). Of this incident light, a small fraction is reflected while the rest is absorbed. The albedo of the moon is about 0.12 (it's dark grey, really).
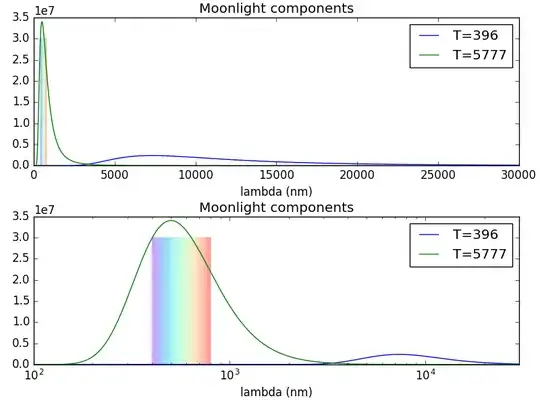
With this assumption, we can use Planck's Law to calculate the apparent "brightness spectrum" of the moon's surface due to black body emission (because the moon is warm) and due to the partial reflection of sunlight. I wrote a little Python program to calculate this, and plotted a graph of the result (note - the upper plot shows a linear wavelength axis; from this you get the sense that the sunlight is bright, but in a narrow range of wavelengths; the lower plot uses a logarithmic axis: this better lets you see the shape of the curves, but you lose your ability to "integrate by eye").
Integrating these two curves, I got the remarkable result that the areas under the two curves (the power due to the reflected sunlight, and the moon's black body radiation) are almost identical (ratio moon/sun = 0.97). I think that's a coincidence. If the moon did not rotate, I would expect it to continue to warm up further (note that the moon, being a sphere, will not be uniformly at 123 C on the sunny side: it will be hotter on the parts that face the sun directly, and hotter again in those parts that were in the sunlight longer; the assumption here that the moon looks like a uniform disk is a significant simplification which may lead to errors of 50% or so - but since 123 C is the given maximum, I think at best this overestimates the temperature that can be reached; unless you could focus your mirror/lens system on just the hottest part of the moon, you would be looking at a "colder" surface, and this would reduce the temperature you could reach).
If the incident sunlight were perfectly in equilibrium with the moon (no rotation), the rate at which sunlight is being absorbed would have to be the same as the rate at which the moon loses heat, so
$$I_{moon}*a = I_{sun}*(1-a)$$
Where $a$ is the albedo (and if $a$ is reflected, $(1-a)$ is the amount of energy absorbed). With an albedo of 0.12, one would expect the intensity of moon light in equilibrium to be $\frac{0.88}{0.12}=7.3$ where we are seeing a ratio of almost exactly 1.0 - from which I conclude that the moon would be able to get hotter if it could spend longer in the sunlight (but the conductivity of moon rock, and the time of exposure, doesn't permit equilibrium to occur).
The code used to generate this is here:
# -*- coding: utf-8 -*-
"""
Simple program to compare components of moonlight
Black body radiation at 123 C
And reflected sunlight
Both with albedo of 0.12 - which is a simplification
@author: floris
"""
import math
from scipy.constants import codata
import numpy as np
import matplotlib.pyplot as plt
D = codata.physical_constants
h = D['Planck constant'][0]
k = D['Boltzmann constant'][0]
c = D['speed of light in vacuum'][0]
def planck(T, l):
p = c*h/(k*l*T)
if (p > 700):
return 1e-99 # hack to prevent underflow
else:
return (h*c*c)/(math.pow(l, 5.0) * (math.exp(c*h/(k*l*T))-1))
albedo=0.12
Tvec=[123+273, 5777] # temperature of moon, sun
Rsun=696.e6 # radius of sun in km
Rsm = 150.e9 # average distance sun to moon
fsun = (Rsun*Rsun)/(Rsm*Rsm) # fractional power of sunlight on moon surface
# vs at the surface of the sun itself
# this shows the reflected sunlight to be a "weak sun"
emVec = [1.0, fsun] # relative intensity of BB radiation
Lvec = np.linspace(1,30000, 30000)*1e-9 # wavelengths: 1 nm - 30 um
# create two figures with an axis, so we can do both lin and log plots
plot1 = plt.figure()
axLin = plot1.add_subplot(211)
#axLin.subplots_adjust(bottom=0.66)
axLog = plot1.add_subplot(212)
plot1.tight_layout(h_pad=2.9)
plot1.subplots_adjust(bottom=0.1)
# create a semitransparent "rainbow plot" to show where visible range is:
axLin.imshow(np.tile(np.linspace(0,1,100),(100,1)), extent=[400, 800, 0, 30000000], aspect='auto', cmap='rainbow', alpha = 0.4)
axLog.imshow(np.tile(np.linspace(0,1,100),(100,1)), extent=[400, 800, 0, 30000000], aspect='auto', cmap='rainbow', alpha = 0.4)
# compute Planck for a range of wavelengths
rmax = 0
R=[]
for ti,T in enumerate(Tvec):
r = []
for l in Lvec:
r.append(planck(T, l))
r = np.array(r)
R.append(r*albedo*emVec[ti])
if rmax==0:
rmax = np.max(r)
imax = np.argmax(r)
r1 = 1.0*r
#plt.semilogy(Lvec*1e9, r/np.max(r),label='T=%d'%T)
axLog.semilogx(Lvec*1e9, albedo*emVec[ti]*r,label='T=%d'%T)
axLin.plot(Lvec*1e9, albedo*emVec[ti]*r,label='T=%d'%T)
axLog.set_xlabel('lambda (nm)')
axLin.set_xlabel('lambda (nm)')
axLog.set_title('Moonlight components')
axLin.set_title('Moonlight components')
axLog.set_xlim((100,30000))
axLog.legend()
axLin.legend()
plot1.show()
# rudimentary integration... sufficiently fine sampling that we can ignore
# the errors for the purpose of this calculation
i_moon = np.sum(R[0])
i_sun = np.sum(R[1])
print('relative intensity moon/sun = %.2f'%(i_moon/i_sun))
So we get roughly equal amounts of energy from the reflected sunlight, and from the moon's heat. This means that the total energy density of the moon is like that of an object that is slightly hotter than the 123 C value used - in fact, and object with that power density would have to be at a temperature of $\sqrt[4]{2}*(123+273)-273=198°C$.
Now an optical system that manages to image the moon in such a way that it illuminates all sides of the target (in effect, making it appear to the target that it is surrounded on all sides by that object - at which point it will end up in thermal equilibrium with that object) can heat that target to the temperature of the object being heated.
Which makes the answer to your question 198°C. This is higher than the temperature of the moon's surface because of the reflected sunlight component which has the same spectral power. This argument does not account for absorption of certain parts of the spectrum by the atmophere; also, it seems to contradict the calculation in this what-if which basically claims (without calculation) that the component of reflected sunlight does not play a role.
Of course it's quite hard to set up a mirror array that gets you to a full $4\pi$ illumination of your target - but that's the best you can do, and then you could boil water.
See also this earlier answer which goes into a bit more depth of estimating temperature when you have an array of mirrors.
According to some forum thread the one needs ~70mW to light a match. And according to the answer given in related question (found by John Rennie) the full moon gives $0.1mW$ using solar cell and mirror with $1m^2$ surface area. I'm not sure why he took solar cell, but his mirror seems to result in 30m in diameter.
There in comments thread some J... guy says the equivalent to 25mm diameter lens in daytime is 17m in diameter lens under moonlight. 25mm lens under sun seems for me to be enough big to burn anything that people use to burn, so lets say for lighting the match we would need 10m lens at night.
But what I've just realised is that the Moon is about 30' in angular diameter and corresponding tangent is around 0.009, that means from the 5 meters distance (average distance from the reflector surface to the match) the projected moon image would be around 50mm in diameter, that is ~200 weaker than if it fully concentrated on the match head. To compensate that we need to take 15 times larger reflector (150m in diameter) but the mirrored beam would also become 15 times longer, that means... no matter how large reflector we take, we'll get only 0.5% of power needed to light the match using light directly. That's probably why the one took solar cell.
But this still does not answer my exact question -- what temperature I can get?