Origin of the force of gravity

Question

Where does exactly gravity come from when bodies exert this force? Does it come from the center of every object or it arises from their surface?

Answer 1

There are a number of perspectives on this. One perspective is that gravitation is not even a force due to the equivalence principle. However, there is the Weyl curvature that induces tidal forces between two bodies or across extended bodies. It is also the case that gravitation is a manifestation of spacetime curvature, but gauge fields or forces are manifestations of curvatures on a principal bundle. Whether gravitation is a force or not is in some ways a matter of definition. If gauge fields are considered to be forces then it probably means we should consider gravitation a force if we are to treat gauge fields and gravitation as existing on the same basis.

I attach the following diagram, which I have presented on a number of occasions. This is a form of the Penrose conformal diagram for the Schwarzschild metric. The horizon of the black hole is the central diagonal cross, and the interior is the wedge at the top, while the wedge at the bottom is considered to be the white hole. The horizontal lines are singularities. The white hole is the aspect of a black hole that emits radiation; it has been thought of as the inverse of a black hole. The regions I and II are exterior regions with different event horizons that present themselves, or the physics surrounding them, to an observer there.

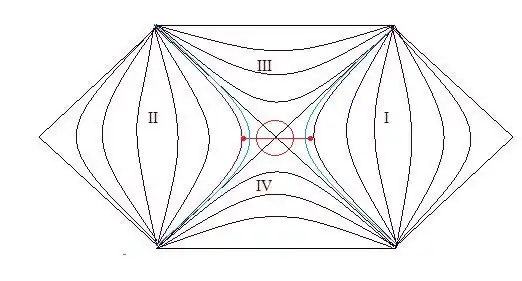
The remarkable thing about general relativity is that it has a structure that gives quantum results. The Bekenstein bound and the laws of black hole thermodynamics is a case in point. The finite temperature and entropy of a black hole strongly suggests some sort of emission process that is quantum mechanical. This lead to Hawking radiation. The Penrose diagram for the black hole is similar. The red circle represents a one loop propagator of a field with Hamiltonian $H$ with phase $exp(-2\pi H/g)$, where the $2\pi$ is a time parameter that defines the circle. The acceleration $g$ is equivalent to the temperature and is $g~=~1/8\pi M$. We then can see the observer in region I will observe the particle emerge from the white hole, rise to some radial distance above the black hole and then falls back down. In region II the loop can be seen as the corresponding anti-particle that rises out of the white hole region and falls into the black hole. The black hole existing in the two regions are then entangled black hole composed of entangled EPR pairs.

Suppose the loop materializes into a particle in region I and II that escapes the black hole as Hawking radiation. The red dots connected by a red segments represent these particles. These particles have gravity fields and they can focus null rays approaching the black hole. This means the horizon radius is reduced and the blue hyperbolic lines represent the horizon due to this emission. The two horizons are no longer connected which reflects some of the entanglement of the black holes being transferred to these particles.

Raamsdonk's paper gives more detailed analysis of this situation. This implies that spacetime is a type of condensate of quantum entanglements. The remarkable feature of how general relativity gives results commensurate with quantum mechanics suggests that ultimately quantum mechanics and general relativity are the same thing.

Curiously, this is also plain vanilla quantum mechanics and not fancy quantum field theory. This can be seen easily with the invariant interval of special relativity. $$ m^2~=~E^2~-~p^2, $$ with $c~=~1$. We assume that this is a highly boosted system along the $z$ direction $p_z~>>~p_x$ and $p_z~>>~p_y$. This means $$ E~=~p_z\sqrt{1~+~\frac{p_x^2~+~p_y^2~+~m^2}{p_z^2}}~\simeq~p_z\left(1~+~\frac{1}{2}\frac{p_x^2~+~p_y^2~+~m^2}{p_z^2}\right). $$ The last term is a form of the classical Hamiltonian for a particle. We may then express this as $$ (E~-~p_z)p_z~=~E'~=~\frac{1}{2}(p_x^2~+~p_y^2~+~m^2). $$ If we use the quantization $p_i~=~-i\hbar\partial_i$ and $E~=~-i\hbar\partial_t$ the invariant interval is the Klein-Gordon equation. This highly boosted or light front system may then be written as $$ i\hbar\frac{\partial\psi}{\partial t}~=~\frac{\hbar^2}{2m}\nabla\psi~+~m^2\psi, $$ which is a Schrodinger equation. The biggest departure is the $m^2$, which is a sort of potential. This means a distant observer watching a relativistic quantum system approach a black hole will witness it redshifted and time dilated into a nonrelativistic quantum system.

This has some interesting implications. Relativistic quantum field theory is formulated according to local fields on spatial surface that have vanishing commutators on that surface. Everything is formulated in this purely local manner. This leads to the idea many particle physicist have that quantum mechanics differs from classical mechanics by commutators. However, nonrelativistic quantum mechanics has a rich depth of nonlocal properties. It is amusing to witness a conversation or debate between a particle physicist and a quantum foundation physicist over this! Quantum field theory can be said to effectively sweep these nonlocal properties of quantum physics away, and to the detriment of physics in general. What this means is that the nonlocal properties of quantum mechanics are equivalent to the nonlocal properties of quantum physics of gravitation.

Answer 2

The gravity applies individually to every bit of mass/energy, independantly.

Imagine you have 5 atoms here, which we’ll label a,b,c,d,e. Now a few miles away there are another 5 atoms, which I'll call A,B,C,D,E. There is a gravitational force between a-A, a-B, a-C, a-D, and a-E, all existing at the same time. Likewise from b to eveything else, etc.

It works if there’s more than 5; say millions or moles or tons of them.

Now imagine the groups of 5 atoms were stuck together to make two solid objects. It doesn’t change anything. The gravity between the two balls is 25 separate atom-sized links all adding their contribution and pulling together. Thus, the force is proportional to the product of the 2 solid object’s masses!

Now if the solid object, which needs to be made of many more atoms than that to be a good approximation of uniform, is a sphere then the center of mass serves as a shortcut. If it’s the size of a basketball, the atoms on one side are a half a foot closer and the atoms on the other side are half a foot farther, and the geometry and values all cancel so you can replace the complex interplay of zillions of atoms in spacially separated positions with an easy calculation by treating it as a single point with a total mass.

But planets and moons are not perfect spheres and there are lumps inside. If you are close up, in orbit say, you will feel the lumps: the thicker techtonic plate in one direction, and a mountain in another. If you are in low orbit the Earth fills half the view! You can point to different continants at different directions, widely separated so you have to turn your head to se one or the other. So you cannot treat the mass as a summary point. The two regions have different mass density and don’t ballance out exactly, so you feel the lumps in your orbit.

This is not specific to the surface. Any variation from uniform and symmetric will do, but things closer to the center will have less separation angle between them so will approximate as being more uniform.

Answer 3

It comes from all mass even from the smallest divisions. Every nucleus or even quark will add to the overall.

Answer 4

It is unknown what physical mechanism "causes" gravity, and indeed the answer to that will depend a lot on the model of gravity that you choose. If you use Newtonian gravity, you assert "action at a distance" that is in some sense caused by the mass itself, but it is known that this is not a complete description, now that we have detected gravitational waves. So one can instead use General Relativity, in which mass/energy creates a curvature in spacetime (that can propagate at the speed of light, as in gravitational waves), but still one does not have a mechanism by which that curvature is "caused." Finally, one can look ahead to new models of gravity, perhaps ones that unify gravity with quantum field theory with the introduction of a gravity-carrying particle called a "graviton." No such theory yet exists, but it seems that when and if it does, the graviton will be able to mediate the force of gravity via the same kinds of "virtual particles" that are now thought to mediate electromagnetic forces (i.e., virtual photons). That would bring us closer to a "cause", though some disparage the concept of a "virtual" particle, given its self-contradictory nature, and also we must admit that no such theory has as yet been successfully created for gravity. But at present, it does seem like gravity is emanated from everywhere that there is mass or energy, so from every piece of an object.