5

(I know whether I understand this or not doesn't matter much to my work & study but am just curious.)

I still can't differentiate in my head kinetics and kinematics (similar thread is found but doesn't explicitly answer to my question yet What is the difference between "kinematics" and "dynamics"?).

Some websites out there say (ex.) explain that force is only considered in kinematics. Does this mean for example Newton-Euler method is in kinetics and Lagrangian is in kinematics?

I also prefer concrete examples in both category.

Community
  • 1
IsaacS
  • 153

3 Answers3

2

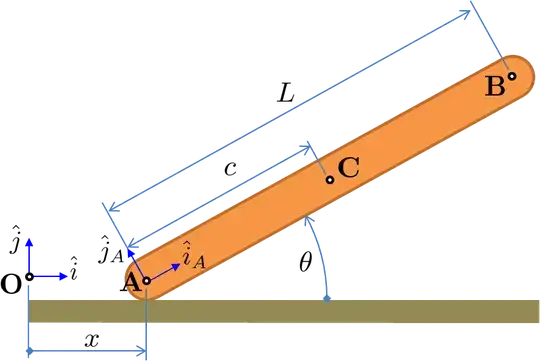
Consider a uniform rod of length $L$ pivoting and sliding on a horizontal plane. KIN1

Kinematics

You want to describe the relationship between the coordinates (and their derivatives) $x$ and $\theta$ and the motion of points A, B, and C.

Position Kinematics

$$ \begin{matrix} \vec{r}_A = x\,\hat{i} & \hat{i} = (1,0,0)\\ \vec{r}_B = \vec{r}_A + L\,\hat{i}_A & \hat{i}_A = (\cos\theta,\sin\theta,0)\\ \vec{r}_C = \vec{r}_A + c\,\hat{i}_A & \hat{j}_A = (\mbox{-}\sin\theta,\cos\theta,0) \end{matrix} $$

Velocity Kinematics

$$ \begin{matrix} \vec{v}_A = \dot{x} \hat{i} & \vec{\omega}_A = \dot{\theta} \hat{k} \\ \end{matrix} $$

$$ \vec{v}_B = \vec{v}_A + \vec{\omega}_A \times (\vec{r}_B-\vec{r}_A) $$ $$ \vec{v}_C = \vec{v}_A + \vec{\omega}_A \times (\vec{r}_C-\vec{r}_A) $$

Acceleration Kinematics

$$ \begin{matrix} \vec{a}_A = \ddot{x} \hat{i} & \vec{\alpha}_A = \ddot{\theta} \hat{k} \\ \end{matrix} $$

$$ \vec{a}_B = \vec{a}_A + \vec{\alpha}_A \times (\vec{r}_B-\vec{r}_A) + \vec{\omega}_A \times (\vec{v}_B-\vec{v}_A) $$ $$ \vec{a}_C = \vec{a}_A + \vec{\alpha}_A \times (\vec{r}_C-\vec{r}_A) + \vec{\omega}_A \times (\vec{v}_C-\vec{v}_A) $$

Kinetics

You want to relate the motion of the center of gravity to the forces acting on the system. Use the Newton-Euler equations of motion for the rod on the center of gravity.

$$\begin{matrix} \vec{F}_A - m g \, \hat{j} = m \,\vec{a}_C \\ (\vec{r}_A-\vec{r}_C)\times \vec{F}_A = I_C \, \vec{\alpha}_A \end{matrix} $$

and the definition of reaction force producing no work

$$ \vec{v}_A \cdot \vec{F}_A = 0 $$

is enough to solve for $\vec{F}_A$, $\ddot{x}$ and $\ddot{\theta}$.

Jose Lopez Garcia
  • 137
  • 7
John Alexiou
  • 40,139
1

You haven't told where you have difficulties understanding such simple thing even after doing some research online. I think, Wikipedia has clear description of both.

Historically, there were three branches of classical mechanics:

  • Statics: The study of equilibrium and its relation to forces.

  • Kinetics: The study of motion and its relation to forces.

  • Kinematics: Deals with the implications of observed motions without regard for circumstances causing them. No force is involved here (The site you have linked refers to Kinetics, not Kinematics).

Earth is a Spoon
  • 5,130
-1

Kinetics: The study of forces that cause motion (ex. torque, gravity, friction, etc.) and can be classified into two groups; Linear and angular motion. Kinematics: The study of describing movement (ex. displacement, time, velocity, etc.)

Gladue
  • 1