If gravitational waves are not absorbed or captured by stars and planets and they keep on propagating through the universe, then it means that there must be a certain amount of gravitational energy pervading the universe. Can one make an estimate of how large this energy density is that has been accumulated over the entire history of the universe? Judging from the amount of energy generated in just one event, such as the one that was recently detected, and the number of such events that must have taken place over the entire history of the universe, one would assume that the energy density may be significant (correct me if I'm wrong). Would this energy density be large enough to affect the cosmic evolution of the universe?
1 Answers
The Bianchi IX cosmology is a model that looks at anisotropic variations on a spaetime. This is what a gravitational wave on a spacetime is. The spacetime at large has the two directions of polarizations of a large scale gravitational wave. We can look at gravitational radiation in cosmology at large by imposing some aspects of the Bianchi IX cosmology on the accelerated expanding spacetime or inflationary spacetime. This will involves some approximations, but we can see some of the features this will produce. We have the standard de Sitter cosmology that for large coordinate time $t$ is approximately $$ ds^2~=~dt^2~-~e^{\alpha(t)}(dr^2~+~r^2d\Omega^2). $$ This is a sort of time dependent conformal transformation on the spatial surface. The standard situation is $\alpha(t)~=~\sqrt{\Lambda/3} t$We may perturb the spatial surface with some functions $\beta_i$ so that $$ ds^2~=~dt^2~-~e^{\alpha(t)}[e^{2\beta_1}dx_1^2~+~e^{2\beta_2}dx_2^2~+~e^{2\beta_3}dx_3^2] $$ where $e^{\beta}$ is a diagonal traceless matrix. Different values of these functions $\beta$ produce anisotripies in the spacetime. We may then write this according to the Bianchi IX spacetime solution with $$ \beta~=~diag\left(\beta_+~+~\sqrt{3}\beta_-,\beta_+~-~\sqrt{3}\beta_-,-2\beta_+ \right) $$ The Ricci curvatures are zero and the type I solution gives the field equations $$ 4\dot\alpha^2~-~\dot\beta_+^2~-~\dot\beta_-^2~=~0 $$ $$ \ddot\beta_{\pm}~-~3\dot\alpha\dot\beta_{\pm}~=~0. $$ This describes linear motion $e^{2\beta}_{ij}~=~(t~-~t_0)^c\delta_{ij}$ of the Kasner model.
I will now consider an approximate form of the more general solution. The entire set of field equations are complicated, but an approximate form with $\beta_+~<<~0$ and considering $\beta_-$ as the same as $\beta_+$ ($\beta_+~-~\beta_-$ really small) in a differential equation for $\beta_+$ gives
$$
\ddot\beta_+~-~3\dot\alpha\dot\beta_+~+~Ce^{\alpha}\beta_+~\simeq~0,
$$
where $C$ is a constant. A numerical graph of this is
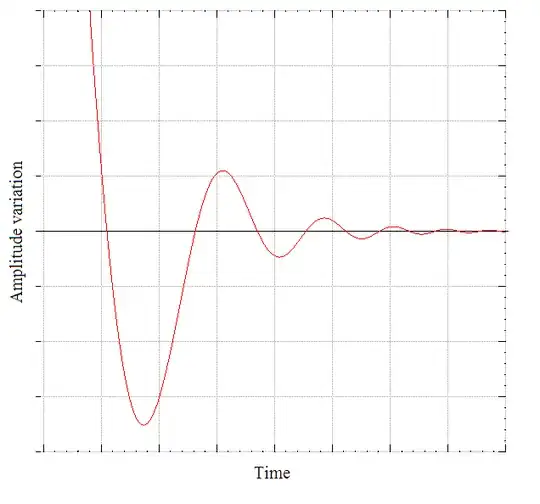
It is evident that the anisotropies are damped out. These would be produced in the inflationary spacetime due to fluctuations, but these would be damped. With the end of inflation this damping would be far reduced and could leave a remnant signature on the CMB surface of last scatter in the cosmology. This was the intent of the BICEPII measurements, and a great fanfare was sounded in the spring of 2014 on this. These anisotropies would reproduce B-modes of a vortex like nature in the polarization of CMB radiation, and back in 2014 is was announced these were found to $6$ sigma. Unfortunately, or fortunately in fact, it has been found that galactic dust can minic this. The dust produces B-modes. This knocked the BICEP data down to about $3$ sigma. The much more difficult task is now to filter real inflationary induced gravity wave B-modes from galactic dust.
- 13,005