2

I recently saw the boards of a flat-Earther on Pinterest. I believe that the notion that the Earth is flat is complete idiocy. I had a feeling that something would be wrong with gravity if the earth was flat, but I wasn't sure what. So that brings me to the question, could a disc, given enough mass, have a gravitational pull, and if so, how would it act?

Qmechanic
  • 220,844
Jun Hayakawa
  • 21

2 Answers2

8

Jun Hayakawa asked: could a disc, given enough mass, have a gravitational pull, and if so, how would it act?

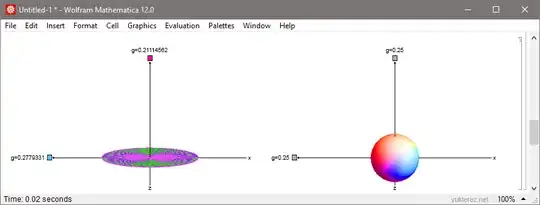
To the side of the disk the gravitational attraction would be higher, and above or below the disk lower than in the vicinity of a sphere or point with the same mass (where the gravitational field is spherically symmetric and therefore the same in every direction). Below you have a disk with M=1 and a sphere also with M=1, and the test particles are at a radial distance of R=2:

comparison of the gravitational fields of a disk and a sphere

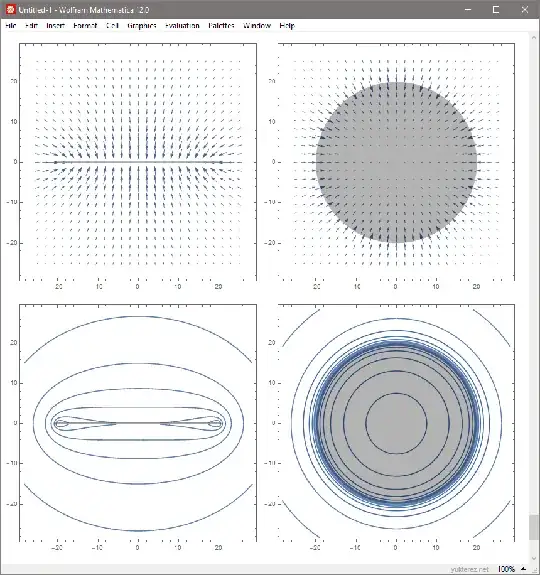
The vector field lines and the surfaces of constant gravitational acceleration look like this for a homogenous disk (in the images below a disk with radius я=20 is lying on the z=0 plane; left: x,z-axes, right: x,y-axes):

gravitational vector field and surfaces of constant acceleration of a homogenous disk

An other thing worth mentioning is that since in the near field the gravitational acceleration is not proportional to 1/R², the orbits may shift in the perihelion:

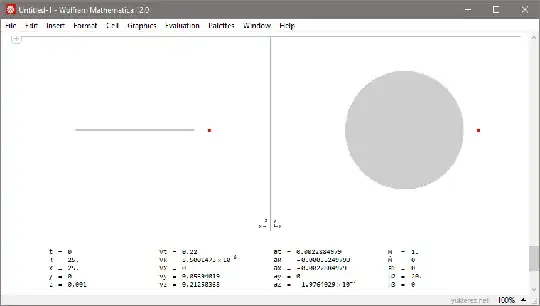
perihelion shift of an orbit in the gravitational field of a disk

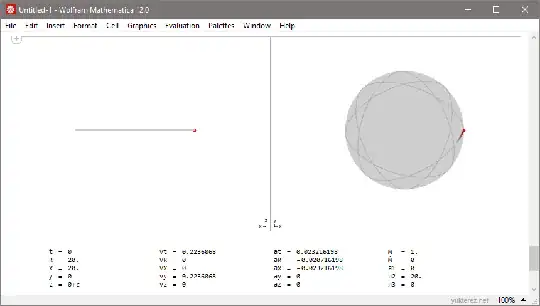
Inside a permeable homogenous disk (for example in a simple galaxy model) the required orbital velocities in the plane of the disc would also be higher than inside a homonenous ball; for example, a test particle starting with the Keplerian circular velocity v⊥=√(GM/R) is not fast enough to stay on a circular orbit when the galaxy is not spherical but disk shaped, and gets dragged into an elliptical orbit:

orbit inside a homogenous disk

For more information here are some references on the subject:

  1. Krogh, Ng & Snyder: The gravitational field of a disk (Pdf)
  2. Lass & Blitzer: The gravitational potential due to uniform disks and rings (Pdf)
  3. Alberti & Vidal: Dynamics of particles in a gravitational field of an annulus (Pdf)
  4. Van Biezen: Gravity with mass distribution (Youtube playlist)
Yukterez
  • 14,655
2

Yes, anything that has mass will exhibit a gravitational field according to Newton's law of universal gravitation, and the strength of the field will be weaker at far distances from the object, but stronger closer to the object, roughly speaking. More precisely, the field will weaken "as $1$ over the distance from the center of mass of the body, squared."$^\dagger$ So yes, a flat earth would have a gravitational attraction, but things would look quite different than the way they look on our round earth. If you were near the edge of the disk, you would appear to be standing almost perfectly sideways since the gravitational field points towards the center of the disk, not straight into the disk, and walking towards the edge would be like climbing a mountain becoming steeper and steeper.

Note that many flat-earthers deny the existence of gravity as I described it here. They instead assert that the flat earth accelerates uniformly upwards at $9.8$ m/s$^2$.

Here is a wonderful VSauce video on YouTube that discusses the flat earth. There is an animation showing what gravity would look like on the disk-shaped planet.

$^\dagger$As the comments below pointed out, the inverse square law does not hold in general.

Alex Ortiz
  • 585