Neutron-Antineutron Annihilation

Question

Is the process $n + \bar{n} \rightarrow \pi^{+} + \pi^{-} + \pi^{0}$ possible?

Answer 1

Within a few MeV, from isospin symmetry of the strong interaction, it is similar to the antiproton proton annihilation which happens even at rest: Role of Delta exchange for proton-antiproton annihilation into two-pion and three-pion channels .

No problem of energy conservation due to the much smaller masses of the pions to the two nucleons.

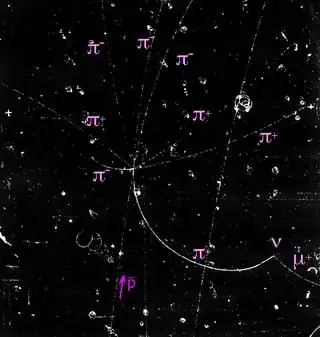
This is an actual bubble chamber photograph of an antiproton (entering from the bottom of the picture), colliding with a proton (at rest), and annihilating. Eight pions were produced in this annihilation. One decayed into a mu + and a neutrino. The paths of positive and negative pions curve opposite ways in the magnetic field, and the neutral leaves no track.

This is antiproton proton, but antineutron-neutron would look the same (impossible to get a beam of antineutrons). Average pion multiplicity at rest is five, two pi0 3 charged (note, average).

Answer 2

It might be suppressed for reasons I am too lazy to examine the process for (symmetry concerns, especially related to rotations), but energy is not a problem. If the two neutrinos have enough kinetic energy, it can be converted into the mass of the pions (among other possibilities, including electron-positron production). In math we're looking for solutions that satisfy all of the following equations: $$\begin{align}E_{\nu} + E_{\overline{\nu}} &= E_{+} + E_{0} + E_{-}, \\ \vec{p}_{\nu} + \vec{p}_{\overline{\nu}} &= \vec{p}_{+} + \vec{p}_{0} + \vec{p}_{-}, \\ m_{\nu}^2 c^4 &= E_{\nu}^2 - c^2 \vec{p}_{\nu}\cdot \vec{p}_{\nu}, \\ m_{\overline{\nu}}^2 c^4 &= E_{\overline{\nu}}^2 - c^2 \vec{p}_{\overline{\nu}}\cdot \vec{p}_{\overline{\nu}}, \\ m_+^2c^4 & = E_{+}^2 - c^2 \vec{p}_{+}\cdot \vec{p}_{+}, \\ m_0^2c^4 & = E_{0}^2 - c^2 \vec{p}_{0}\cdot \vec{p}_{0}, \ \mathrm{and} \\ m_-^2c^4 & = E_{-}^2 - c^2 \vec{p}_{-}\cdot \vec{p}_{-}. \end{align}$$ That's 9 equations and 12 unknowns, so the space of possible solutions has 3 dimensions.

Answer 3

Nice question. As anna pointed out if neutron and anti-neutron are throwing together with some MeV, no question they will splash into different particles and EM radiation.

But what means annihilation? Usually it means the attraction of charged particles from different sign, for example an electron and a positron. During the approach they emit EM radiation and this process - like it happens between electron and proton or between positron and anti-proton - doesn't stops at some distance.

The neutron and the anti-neutron will not approach by themself and due to noexisting electric fields no annihilation takes place. There is an elaboration of mine about how the approach of charged particles can be modelled and due to this a neutron - antineutron annihilation is impossible (from the above definition of what an annihilation is). The existence of electric fields allows particles to get bonded or to be repealed.