Transferring force through a string, including gravity

Question

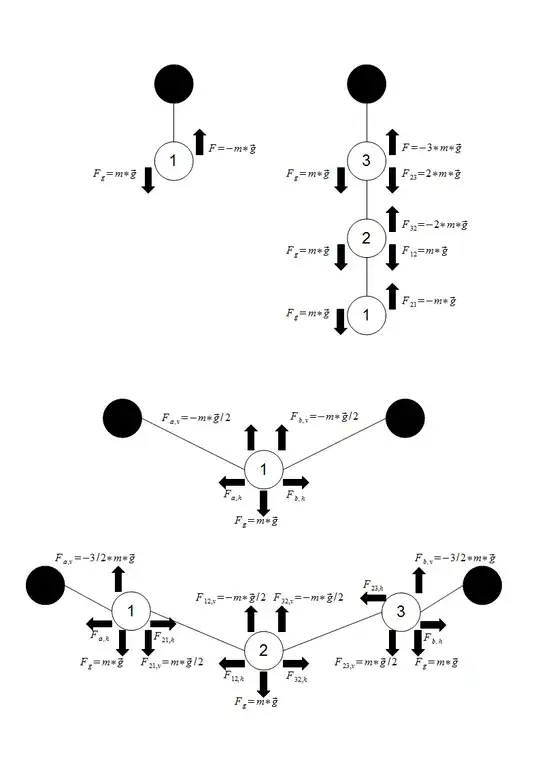
I couldn't think of a better title to describe this confusion that I have.

Say you pick up a string and pull on both ends so that it is rigid. The string is a collection of an infinite number of objects. For simplicity, assume there are $n$ objects for some large integer $n$, each of which has mass $m$, and number the objects $A_1$, $A_2$, ..., $A_n$ from left to right. Maybe we can take the limit as $n$ goes to infinity; I don't know how to rigorize this.

Your left hand exerts some force $\vec{F}$ onto $A_1$. The only other two forces on $A_1$ are gravity and the force $\vec{F}_{21}$ from $A_2$, since $A_1$ is only in contact with $A_2$. Gravity is $m\vec{g}$. Since the string is not moving, the sum of the forces on $A_1$ is $\vec{0}$, so
$$\vec{F}_{21}+\vec{F}+m\vec{g}=\vec{0}$$ $$\vec{F}_{21}=-\vec{F}-m\vec{g}$$

By Newton's Third Law, the force $\vec{F}_{12}$ from $A_1$ onto $A_2$ equals $-\vec{F}_{21}$, which is $\vec{F}+m\vec{g}$. The only other two forces on $A_2$ are $m\vec{g}$ and the force $\vec{F}_{32}$ from $A_3$ onto $A_2$, so
$$\vec{F}+m\vec{g}+m\vec{g}+\vec{F}_{32}=0$$ $$\vec{F}_{32}=-\vec{F}-2m\vec{g}$$

If we keep going, we add an $m\vec{g}$ each time, until we get that the force from our right hand onto $A_n$ is $-\vec{F}-nm\vec{g}$, which is a lot more than $\vec{F}$, not to mention that $n$ is supposed to go to infinity.

What is wrong with my logic? Do my hands somehow exert $-m\vec{g}$ on each object?

Answer 1

Since a picture sometimes says more than a thousand words:

The first example in the upper left is just a mass hanging on a fixed point(/your hand). Gravitation pulls downwards with $m*\vec{g}$ and therefore the fixed point needs to exert a force $-m*\vec{g}$ on the mass.

The second example in the upper right are multiple masses hanging on each other. Here it is easiest to start from the lowest one (1). Gravitation pulls downwards, so something needs to pull with the same force upwards. And the only possible force here is $F_{21}$ from the connected mass (2). Looking at mass (2) we have gravitation ($m*\vec{g}$), the force from (1) ($m*\vec{g}$) and the force from (3), which therefore needs to be $-2*m*\vec{g}$.
The same principle applies to mass (3), so overall the fixed point/hand needs to exert a force of ($3*m*\vec{g}$) on the rope/chain of masses. Which is pretty clear, because thats the weight of the chain.

In the middle of the picture you see an example of a mass hanging on two fixed points (with massless ropes). We have gravitation pulling downwards with $m*\vec{g}$, so each of the ropes needs to exert a vertical component of $-m*\vec{g}/2$. They might have additional horizontal components $F_{a,h}$ and $F_{b,h}$. In order to have a static system of course it needs to be $F_{a,h} = -F_{b,h}$.
So with each of your hands you would have to exert an overall force of $F_h + m*\vec{g}/2$.
Note that the vertical components again add up to the weight of the 'chain'.

The last example is the trickiest one and the one you were looking for. Leaving aside the horizontal forces which are all equals (besides a sign), it is again the easiest to start in the middle. The gravitational force on mass (2) is 'split' between the two neighbouring masses (1) and (3). Each of them kind of 'adds' its own mass to the overall force needed to hold the system static, until we are finally left with two times $\frac{3}{2}*m*\vec{g}$ which is again the weight of the mass chain.

So basically yes, your hands exert a force $-n*m*\vec{g}$. If they would not, the rope would just fall down. Or better, the rope falls downwards until they actually do, which is the reason why no rope can ever be totally straight.
This vertical force is propagated through the chain of masses, but for every mass one portion $m*\vec{g}$ is 'lost' in order to keep this small mass from falling.

Answer 2

If you divide the string into $n$ parts then each part has mass $m/n$, where $m$ is mass of string. So beginning with one end of the string and proceeding with your argument, by the time you reach the other end the force will be $-\textbf{F}-n\times (m/n)\textbf{g}=-\textbf{F}-m\textbf{g}$, which is as it should because when you consider the string in its entirety, given that it is stationary, vector sum of forces on it must be zero: $\textbf{F}_{one~end}+\textbf{F}_{other~end}+m\textbf{g}=\textbf{0}$.