Could a causal mass decrease cause antigravity, i.e. repulsive gravity?

Question

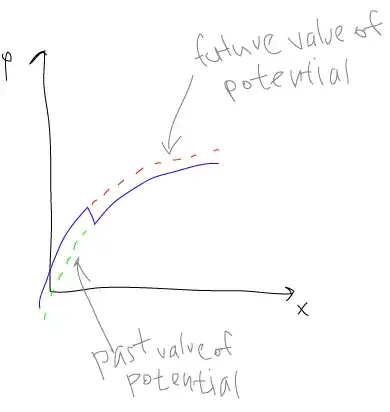
Suppose some mass $M$ is located at rest in some point of space. It creates gravitational potential well, which attracts test bodies towards $M$:

Now suppose that the mass of a body drastically decreases several times to $m << M$, for example if the mass is radiated away as gravitational waves as in the recent black hole merger detected by LIGO. This causes the potential well become shallower. But this can happen at up to the speed of light, so there should an outgoing wave running on the potential plot:

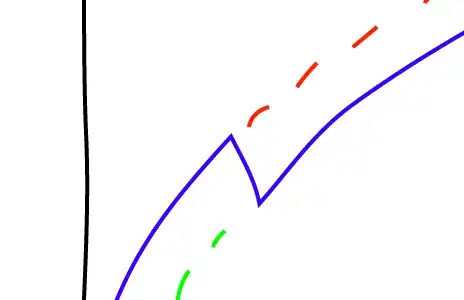
Now regard the area on the wave:

$- \nabla \phi$ is directed outward here. i.e. body feels anti-gravity, i.e. repulsive gravity!

Does this effect occurs in reality, for example when two black holes merge? The mass of these holes is decreased due to gravitational wave emission.

I would say that this is the same as gravitational waves pressure, but this looks as different nature. GW are quadrupolar, while here we see monopolar pure newtonian plot.

So, will there be some additional gravitational repulsion in reality?

Answer 1

No. In newtonian gravity we can predict what would happen if mass was magicked out of existence. However, in general relativity this gets ill-defined, so we have to stick to what's physically possible: flinging out the mass as mass or energy. For this example we have 75% of the mass sent out all at once at t=0 as gravitational waves or photons (at light speed). Furthermore, we assume that the gravity is weak enough so that there isn't strong space-time distortion (escape velocities are << c).

Your diagram is slightly wrong. The shell of radiation is not associated with a jump in potential, it is associated with a jump in force. We can easily integrate this to get the potential:

There is never a repulsion zone. At each point, the gravity force suddenly and permanently reduces to 25% of it's original value as the shell of radiation passes. After this happens the potential gradually increases, converging to the t=Inf curve but the slope of the curve (the force) is constant.

Edit:

Potential is a property that is inferred by integrating from the given location to infinity, assuming that the shell could somehow be stopped. It's slope at each point and time gives the force on a particle hovering at that point, but the overall energy at a point inside the shell and the fact that it increases toward the t=Inf curve is meaningless because there is no way for a particle to outrun the shell. A spaceship inside the shell would ignore the shell and use the t=Inf potential curve for flight calculations.