19

I'm having a hard time understanding the distortion model of OpenCV. They use "radial" coefficients $k_n$ and "tangential" coefficients $p_n$ among others that I am not interested in.

$$ x' = x (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2 p_1 x y + p_2(r^2 + 2 x^2) \\ y' = y (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1 (r^2 + 2 y^2) + 2 p_2 x y $$

To understand this, I separated the two terms into what $\Delta$ offset they produce, here's how that looks for $x$:

$$ \begin{array}{rlcccc} x' &= x &+ &\underbrace{x(k_1 r^2 + k_2 r^4 + k_3 r^6)} &+ &\underbrace{2 p_1 x y + p_2(r^2 + 2 x^2)}\\ &= x &+ &\Delta x_{radial} &+ &\Delta x_{tangential} \end{array} $$

Then I plotted those values as a vector field with octave (similar to Matlab).

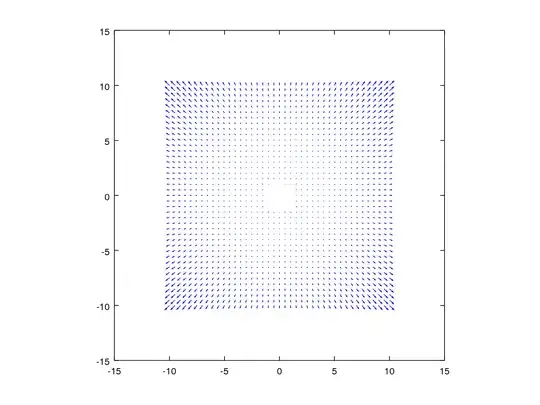
Radial Distortion

function radialDistortion (k1, k2, k3)
    max = 10;
    [x, y] = meshgrid(-max:.5:max);
    r2 = x.**2 + y.**2;
    k = k1*r2 .+ k2*r2.**2 .+ k3*r2.**3;
    quiver(x, y, x.*k, y.*k, 0);
    axis("square");
endfunction

Called with

radialDistortion(0.0002, 0, 0)

produces the following

radial distortion

I get it, this is radial to the optical axis, thus being point symmetric to the center (where the optical axis is). This wasn't too difficult.

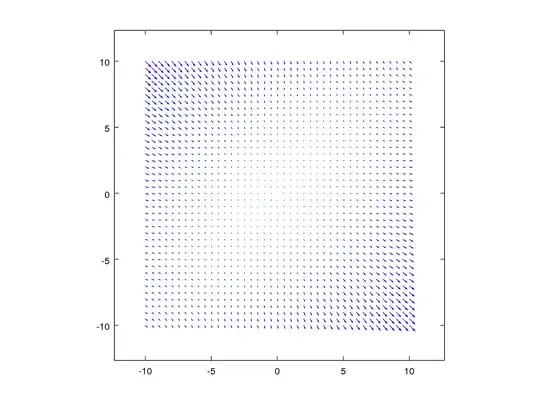
Tangential Distortion

function tangentialDistortion (p1, p2)
    max = 10;
    [x, y] = meshgrid(-max:.5:max);
    r = x.**2 + y.**2;
    xy = x.*y*2;
    quiver(x, y, xy*p1 + (r+2*x.**2)*p2, xy*p2  + (r+2*y.**2)*p1, 0);
    axis("square");
endfunction

Called with

 tangentialDistortion(-.0007, .0007)

produces this

tangential distortion

How is this "tangential" to anything? To me, it looks like it is correcting for a lens that's tilted (rotated around the bottom-left-to-top-right diagonal) which agrees with the reason for this distortion given in the literature: lens misalignment.

Does that mean it's tangential to the surface of the lens?

In the end, it's some mathematical model that describes some optical phenomenon in order to correct it. But I'd like to understand why this is called "tangential".

If the position of P' is also displaced tangentially relative to CP (along the tangent to the circle of radius CP), the distortion is said to be tangential.

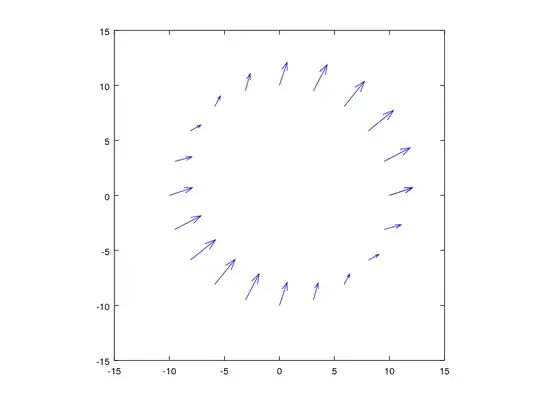
No, it isn't. I modified the above function to show the "tangential" displacement of points that are on a circle.

function tangentialDistortionOnCircle (p1, p2)
    radius = 10;
    x = radius * cos(0:2*pi/20:2*pi);
    y = radius * sin(0:2*pi/20:2*pi);
    r = x.**2 + y.**2;
    xy = x.*y*2;
    quiver(x, y, xy*p1 + (r+2*x.**2)*p2, xy*p2  + (r+2*y.**2)*p1, 0);
    axis([-radius-5 radius+5 -radius-5 radius+5 ], "square");
endfunction

Called with these parameters:

tangentialDistortionOnCircle(.007, .007)

gives this result

tangential distortion on a circle

This doesn't look like a tangential displacement to me at all. If it was, it would look like a swirl around the center. But that's not the case.

null
  • 385

3 Answers3

14

Take the position of a point P on the image relative to the geometric image center C. Assume C remains undistorted in the lens produced image, but P is distorted into P'.

If the position of P' is only distorted radially along direction CP, the distortion is said to be radial.

If the position of P' is also displaced tangentially relative to CP (along the tangent to the circle of radius CP), the distortion is said to be tangential.

See for instance "Camera Calibration with Distortion Models and Accuracy Evaluation" (IEEE Transactions On Pattern Analysis And Machine Intelligence), especially Figs.2 & 3 (pg. 968) and Fig.4 (pg.969).

udrv
  • 10,551
  • 1
  • 26
  • 35
0

The tangential distortion corrects for tilts of the image plane after radial distortion. Imagine subtle manufacturing flaws where the optical elements not aligned with the imaging plane. Tangential coefficients correct for this imperfection. This is why it seems like a rotation of the imaging plane. The net result of both radial and tangential warps should be a pinhole model which you can then apply classic intrinsics parameters to once you locate the principal point.

dorbie
  • 1
0

The pertinent papers on tangential distortion have references that go all the way back to Conrady's 1919 paper on "decentered lens systems." In this paper Conrady talks about distortion that is caused by decentering error of a multi-element lens system. Most modern cameras have multi element lenses. Brown's paper from the 1960's has the form we see in OpenCV today. This equation almost models a tilted sensor except for the r squared terms, but it is intended to model a decentered lens system. Brown calls it Decentering Distortion. Brown says this in his paper: "A significant degree of decentering will introduce both tangential distortion and asymmetric radial distortion."

Geoff
  • 1