Regarding the Symmetricom SA.45s Quantum™ Chip Scale Atomic Clock, is it accurate enough to test time dilation if I place one at sea level, and one on a mountain? It's accurate to 3.0⋅10−10 per month.
Asked
Active
Viewed 6,636 times
4 Answers
37
According to my calculations, no.
Let's treat the earth as perfectly spherical, then the relative error at which time passes for the observer on the ground $r_1=R_E$ and on the mountain of height $h$, $r_2=R_E+h$, is
$$ \frac{t_2-t_1}{t_1}=\frac{t_2}{t_1}-1 = \frac{\sqrt{1-r_s/r_2}}{\sqrt{1-r_s/r_1}}-1 $$
where $r_s=2GM_E/c^2$.
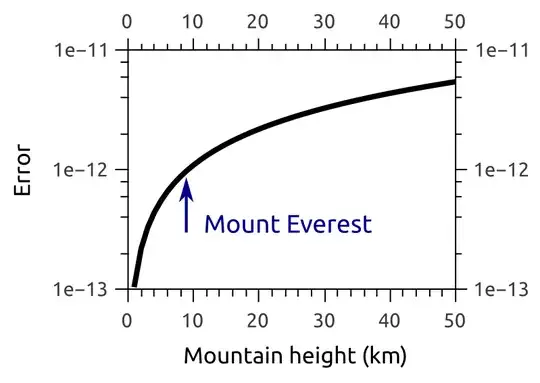
Here is a log-plot of this error versus the mountain height $h$:
It would seem that the time dilation error, even on Mount Everest, would be at least a few orders of magnitude too small for this device to resolve.
lemon
- 13,320
22
When gravity isn't very strong, i.e. as long as we aren't near any black holes, The relative time dilation between two points is related to the difference in their gravivitational potential energy by the weak field equation:
$$ \frac{dt_a}{dt_b} = \sqrt{1 + \frac{2\Delta\Phi_{ab}}{c^2}} \tag{1} $$
where $\Phi$ is the Newtonian gravitational potential energy per unit mass. Near a spherical mass $M$ this is given by:
$$ \Phi = -\frac{GM}{r} $$
or if the distance is small the difference is just:
$$ \Delta\Phi \approx gh $$
where $h$ is the vertical distance between the points $A$ and $B$. Since we're just trying to get a rough idea of whether the clocks will work lets use this approximation for $\Delta\Phi$ in which case our equation (1) becomes:
$$ \frac{dt_a}{dt_b} \approx \sqrt{1 + \frac{2gh}{c^2}} \tag{2} $$
and since $gh/c^2$ is small we can use a binomial expansion to expand the square root to give.
$$ \frac{dt_a}{dt_b} \approx 1 + \frac{gh}{c^2} \tag{3} $$
Now I'm not totally sure what the cited accuracy of $3 \times 10^{-10}$ per month means, but I'm guessing that it means the ratio of the measured time to the real time over one month would be $1 \pm 3 \times 10^{-10}$. In that case our calculation is now very easy, because it means that for the gravitational time dilation to be detectable:
$$ 3 \times 10^{-10} \lt \left|\frac{gh}{c^2}\right| $$
or:
$$ \left|h\right| \gt 3 \times 10^{-10} \frac{c^2}{g} $$
And feeding in the numbers gives me:
$$ \left|h\right| \gt 917\,\text{km} $$
Actually this height is large enough that our approximation of using $\Delta\Phi=gh$ breaks down, and when you do the calculation properly you find the minimum value for the height difference $h$ is around $5,000$ km. But either way your chip scale atomic clock isn't useful for measuring time dilation unless you can find an exceedingly high mountain.
For some perspective it's worth comparing this result to the well established time dilation experienced by GPS satellites. The gravitational time dilation experienced by a GPS satellite is about $47\mu\text{s}$ per day, with is a drift of about $5\times 10^{-10}$, so it is just detectable by your chip. However GPS satellites orbit at a height of about $20,000$ km.
John Rennie
- 367,598
6
Regarding the Symmetricom SA.45s Quantum™ Chip Scale Atomic Clock, is it accurate enough to test time dilation if I place one at sea level, and one on a mountain? Its accurate to 3.0E-10 per month
Yes, but you will have to conduct the experiment over a longer period of time, and using a high mountain so the error in the clock is swamped by the effects of time dilation. The atomic clock you are looking at has an accuracy of ±5.0E-11.
Here's an example of someone with an accuracy only two orders of magnitude higher measuring the time dilation occurring at a height of only 2km:
http://www.leapsecond.com/great2016a/index.htm
This example shows six clocks being used, three at the top of the mountain, three at the bottom, over a period of 24 hours, with a height of 2km. By using several clocks you increase redundancy in case equipment failure occurs, but you also increase accuracy - assuming the error is distributed (and you can't simply assume that, but it may be good enough for your purposes) then the more clocks you use in your calculations, the more accuracy you gain.
You may have to use your less accurate clocks over a much longer period of time, and at a much higher height, given your larger error, but they are accurate enough to measure time dilation empirically.
The original experiment resulted in some conference talks and papers:
Adam Davis
- 1,510
0
As I understand the specification of the accuracy of the mentioned clock, the actual accuracy is $\lambda t =\frac{3.0 e^{-10}}{30x24x60x60}$ = $1.15 e^{-16}$. If this is correct, you should be able to detect the time dilation at much lower altitude than has been calculated (in the neighborhood of 0.5 meter).
As you can see, the result depends on what the accuracy specification means.
Guill
- 2,573