The question is, if two following phenomena are thought to effect to the motion of the planet that orbits a star:
- Celestial body is pulled by some massive star by ordinary Newtonian gravity:
$$ m \frac{d^2r}{dt^2} = - G \frac{Mm}{r^2} $$
- There is additional radial velocity component
$$ \frac{dr}{dt} = kr\ ,\qquad k << 1 $$ or (linear approximation): $$ r(t) = r_0 (1+ kt) , k << 1\ , $$
that pulls the body $m$ away from the mass $M$ - and that is independent from the gravity (that means it happens also in zero gravity), what kind of solutions would these 2 rules give for orbits and can the orbits be stationary in some situations?
The Newtonian gravitation law only, when the mass $M \gg m$, would result a Keplerian orbit: $$ r(\theta) = \frac{a(1-e^2)}{1 + e\cos(\theta)}$$ that is circle, ellipse, hyperbola, or parabola.
Partial answers:
A. At least the circular motion equilibrium can be maintained at the start simply by demanding that the initial velocity of the body to be not exactly tangential, but have a small radial component inward:
$$ v_{initial} = v_{tan} + v_{r}\ , $$ where $$ v_{r} = -kr $$
Now the radial component of initial velocity would cancel the radial velocity $kr$ at initial time. What would yield to the familiar equilibrium equation for circular motion:
$$ v^2/r = GM/r^2 $$
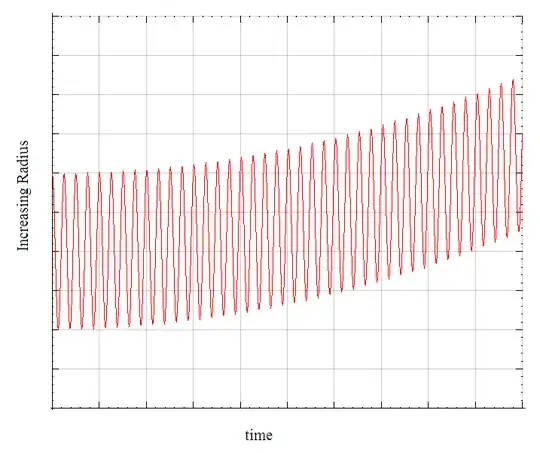
B. Also, when the planet is put into aphelion point of the orbit, where the Newtonian gravitation is in then minimum and according Newtonian gravitation law its velocity would be perpendicular to $r$ and in the minimum, the initial velocity should be slightly inward from the tangential velocity $v$, if this point would be the true aphelion point. From this initial condition, the first guess is that the resultant orbit or trajectory should be then somewhere between the aphelion circle $r_{max}$ and perihelion circle $r_{min}$ -at least during the first cycle.
The first guess for the orbit equation is simply: $$ r(\theta) = \frac{a(1-e^2)}{1 + e\cos(\theta)}(1+kt)$$ or $$ r(\theta) = \frac{a(1-e^2)}{1 + e\cos(\theta)}e^{kt}\ ,$$ if nothing else (e.g gravity of other planets, orbital decay, etc) effect on the motion.
The reason why I ask this question is that I would like to think what would happen if the cosmological expansion of the universe would effect on the celestial mechanics. I have read that this is not thought to be true however, cosmic expansion is not effecting the solar system. But if it would be true, the cosmic expansion would be described approximately by equations: $$r = r_0(1 + Ht) $$ that is linear approximation when $t$ is small, or $$ \frac{dr}{dt} = Hr\ , $$ which is another approximation when $t$ is small, whose solution is exponential function.
And the value for $H$ would be around $H = 2.20 \times 10^{-18}\, \mathrm{s}^{-1}$ or $H = 6.93 \times 10^{-11}\, \mathrm{year}^{-1}$, that is simply the Hubble constant is the units [1/s] and [1/year].
With this value for $k$, for example Earth-Moon distance 384000 km should increase by 2.63 cm/year, and Earth-Sun distance $150\times10^6\, \mathrm{km}$ would increase by 10.4 m/year, if nothing cancels this effect.
The observed values are 3.8 cm/year (radar measurements) and 10.4 cm/year (That is 100 times smaller. I don't know how the value of AU is actually measured). The Moon-Earth system is thought to separate due to tidal forces, but it is unclear to me how much this effect really contribute to the increase of Earth-Moon distance.