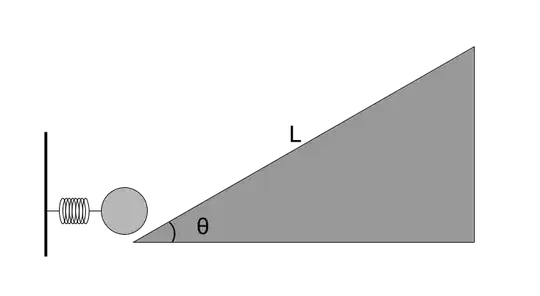
A book that I am using to study poses the following problem:
Suppose you wish to use a spring with a force constant $k$ to launch a spherical ball or radius $r$ and mass $m$ up a ramp of inclination $\theta$ and hypotenuse $L$. Suppose also that the ball stops just at the top of the ramp so that it travels a distance $L$, and that friction is sufficient for the ball to roll without slipping immediately after launch. What distance should the spring be compressed?
It is clear to me that in the absence of friction that one simply relates the potential energy stored in the spring to the gravitational energy the ball obtains at the top of the ramp. My book states that even when the ball rolls without slipping as a result of friction the approach is still the same.
I find this last statement confusing since friction is a non-conservative force, so some energy should be lost, and the ball will not rise to the same height. Is this reasoning incorrect? Am I misinterpreting "rolling without slipping"?