Why are the harmonics of a piano tone not multiples of the base frequency?

Question

I was trying to figure out which piano keys were being played in an audio recording using spectral analysis, and I noticed that the harmonics are not integer multiple of the base note. What is the reason for this?

---

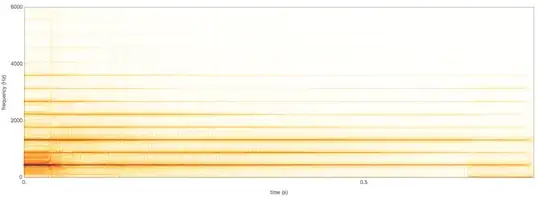
Take a look at the spectrogram of a clean sample from a single piano key. I am using Piano.ff.A4 from here.

The following is the same as above, with a superimposed reference grid of $ 440 ~\mathrm{Hz}$. As you can see, the harmonics have increasingly higher frequencies than integer multiples of $440 ~\mathrm{Hz}$.

At this point you might think that the actual base frequency is just slightly higher than $440 ~\mathrm{Hz}$. So let us make a different reference grid, which lines up with the harmonic at ~$5060 ~\mathrm{Hz}$.

You can now clearly see that they aren't actually integer multiples of a base frequency.

Question: What is the explanation for this? I am looking both for simple high-level explanations of what is happening, and more in-depth, instrument specific ones, which could maybe allow me to attempt to calculate the harmonics.

My first reaction was that this must be some non-linear effect. But you can see that the harmonics do not change frequency at all as time passes and the sound gets quieter. I would expect a non-linear effect to be pronounced only in the loudest part of the sample.

---

Update – I measured the frequencies using peak detection on the Fourier transform from 0.3 to 0.4 seconds in the sample. This table compares the measured values with integer multiples of 440:

meas.   int. mult.
440.    440.
880.    880.
1330.   1320.
1780.   1760.
2230.   2200.
2680.   2640.
3140.   3080.
3610.   3520.
4090.   3960.
4570.   4400.
5060.   4840.
5570.   5280.

Answer 1

This effect is known as inharmonicity, and it is important for precision piano tuning.

Ideally, waves on a string satisfy the wave equation $$v^2 \frac{\partial^2 y}{\partial x^2} = \frac{\partial^2 y}{\partial t^2}.$$ The left-hand side is from the tension in the string acting as a restoring force.

The solutions are of the form $\sin(kx - \omega t)$, where $\omega = kv$. Applying fixed boundary conditions, the allowed values of the wavenumber $k$ are integer multiples of the lowest possible wavenumber, which implies that the allowed frequencies are integer multiplies of the fundamental frequency. This predicts evenly spaced harmonics.

However, piano strings are made of thick wire. If you bend a thick wire, there's an extra restoring force in addition to the wire's tension, because the inside of the bend is compressed while the outside is stretched. One can show that this modifies the wave equation to $$v^2 \frac{\partial^2 y}{\partial x^2} - A \frac{\partial^4 y}{\partial x^4} = \frac{\partial^2 y}{\partial t^2}.$$ Upon taking a Fourier transform, we have the nonlinear dispersion relation $$\omega = kv \sqrt{1 + (A/v^2)k^2}$$ which "stretches" evenly spaced values of $k$ into nonuniformly spaced values of $\omega$. Higher harmonics are further apart. We can write this equation in terms of the harmonic frequencies $f_n$ as $$f_n \propto n \sqrt{1+Bn^2}$$ which should yield a good fit to your data. Note that the frequencies have no dependence on the amplitude, as you noted, and this is because our modified wave equation is still linear in $y$.

This effect must be taken into account when tuning a piano, since we perceive two notes to be in tune when their harmonics overlap. This results in stretched tuning, where the intervals between the fundamental frequencies of different keys are slightly larger than one would expect. That is, a piano whose fundamental frequencies really were tuned to simple ratios would sound out of tune!

Answer 2

In plain English, there is stiffness at the ends of the strings where they are fixed in place, which makes the string's frequency of vibration slightly higher (sharper)—effectively shortening the length of the string slightly, for all practical purposes. And the resistance to bending is dependent on the frequency. It behaves more “stiffly” with regard to higher frequencies, reducing the string’s effective lengths more and more for each higher and higher frequency harmonic (“partial”). Therefore the upper partials go effectively sharper in pitch, the higher they get.

All stringed instruments exhibit this effect to some extent, and it’s part of the reason realistic piano sounds were hard to synthesize electronically on early synthesizers… when all the harmonics are in tune, the timbre sounds “deader” and less rich.

A real-life example of this would be guitar strings, which eventually go “dead” as you use them, and don’t sound as good as new strings. This is because the cumulative effect of playing them makes them more and more soft and flexible, reducing the stiffness at the fixed ends and making the upper partials more in tune with the fundamental. This sounds “duller”, much less rich in tone then new, much stiffer strings.

It also means that pianos have to be “stretch tuned”… low notes are tuned slightly flat, and high notes are tuned slightly sharp. Otherwise, playing a $\text{C1}$ and a $\text{C6}$ at the same time would sound slightly out of tune, as the partial of $\text{C1}$ closest to $\text{C6}$ would be slightly sharper than $\text{C6}$'s mathematically precise frequency of $2^5$ times the frequency of $\text{C1}$*, resulting in an audible, out-of-tune-sounding “beat” of the partial against the $\text{C6}$’s root, just like two strings whose fundamentals are close but not exactly in tune. Tuning $\text{C6}$ slightly sharp by the same amount that $\text{C1}$’s $6$-octave partial is sharp, ironically, makes the piano sound more in tune.

EDIT: *A comment below drew my attention to the fact that I had originally made a mistake here. The frequency of $\text{C6}$ is $2^5$ times the frequency of $\text{C1}$, because each octave is a doubling of frequency. In terms of frequency:

• $\text{C2} = 2 \ \text{C1} (=2^1 \ \text{C1})$
• $\text{C3} = 2 \times 2 \ \text{C1} (=2^2 \ \text{C1})$
• $\text{C4} = 2^3 \ \text{C1}$
• $\text{C5} = 2^4 \ \text{C1}$
• $\text{C6} = 2^5 \ \text{C1}$

So that's where the $2^5$ comes from.

Answer 3

Carrying out the Fourier transform, I get a slightly different result for the frequency spectrum than 'knzouh'. I used $u$ instead of $y$ and $c$ instead of $v$, so the PDE becomes:

$$u_{tt}=c^2u_{xx}-Au_{xxxx}$$ Fourier transforming the equation: $$F\{u_{tt}\}=F\{c^2u_{xx}\}-F\{Au_{xxxx}\}$$ Transforming $x$ to $k$: $$\hat{u}(k,t)=\int_{-\infty}^{+\infty}u(x,t)e^{-ikx}dx$$ $$\int_{-\infty}^{+\infty}u_{tt}(x,t)e^{-ikx}dx=\frac{\partial^2}{\partial t^2}\hat{u}(k,t)$$ $$F\{c^2u_{xx}\}=c^2(ki)^2\hat{u}(k,t)=-c^2k^2\hat{u}(k,t)$$ $$F\{Au_{xxxx}\}=A(ki)^4\hat{u}(k,t)=Ak^4\hat{u}(k,t)$$ Inserting we get:

$$\frac{\partial^2}{\partial t^2}\hat{u}(k,t)=-c^2k^2\hat{u}(k,t)-Ak^4\hat{u}(k,t)$$ $$\frac{\partial^2}{\partial t^2}\hat{u}(k,t)=-k^2(Ak^2+c^2)\hat{u}(k,t)$$ Call: $$\hat{u}(k,t)=U(t)$$ So $$U''(t)+k^2(Ak^2+c^2)U(t)=0$$ $$U(t)=c_1\sin(k\sqrt{Ak^2+c^2}t)+c_2\cos(k\sqrt{Ak^2+c^2}t)$$ $$\omega=2\pi f=k\sqrt{Ak^2+c^2}=kc\sqrt{\Big(\frac{A}{c}\Big)^2k^2+1}$$ $$f_n \propto n \sqrt{Bn^2+1}$$

Answer 4

Note also that the strike point of the hammer is not at the vibrational center of the string. This means that the hammer will excite the string in modes that have to do with the distance between the strike point and the end points of the string. This adds anharmonic content to the fourier decomposition.

Note also that the wound strings on a piano are taper-wound i.e., the outer wraps that add mass are terminated before the string makes it to the end, so the only part of the string that is in physical contact with the termination is the core of the string and not the wraps. this is supposed to reduce the flexural "clamping" effect of the termination.

A very complex business!