Problems in the relation $a=v\frac{\mathrm{d}v}{\mathrm{d}x}$

Question

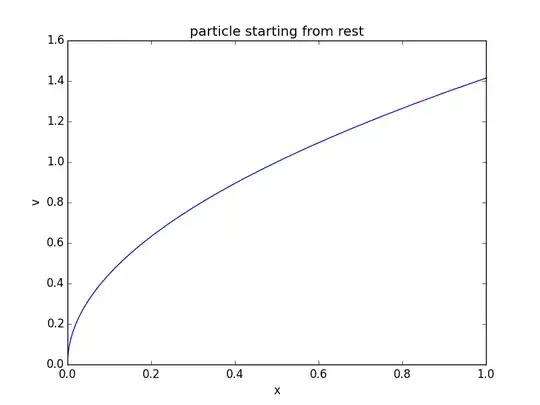
We all know $a = \frac{\mathrm{d}v}{\mathrm{d}t}$. A little application of the chain rule leads to the relation $$a=v\frac{\mathrm{d}v}{\mathrm{d}x}$$ But the above equation shows that $a=0$ whenever $v=0$. And this must be wrong, as when we throw something vertically from the earth surface it stops and then returns due to gravity. There is always an acceleration in the downward direction.

I have come up with two possible ways to solve this problem:

1. We know that $v = \frac{\mathrm{d}x}{\mathrm{d}t}$, so whenever $v=0$ then $\mathrm{d}x=0$ (i.e. no displacement in that infinitely small time). Also, $$a = \frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t}$$ only if $\mathrm{d}x$ is not equal to $0$, as multiplying both numerator and denominator with $0$ will make it $0/0$ (undefined). Or multiplying by $0/0$ is not equivalent to multiplying by $1$.

   Now since $\mathrm{d}x=0$ whenever $v=0$, therefore we can not write $a = v\frac{\mathrm{d}v}{\mathrm{d}x}$ when $v=0$.

2. If we plot a $v$-$x$ curve for the motion, whenever $v=0$, as explained, $\mathrm{d}x=0$. Therefore, at that instant $\frac{\mathrm{d}v}{\mathrm{d}x}$ (the slope of the $v$-$x$ curve) will be not defined (as $\mathrm{d}x=0$), therefore the equation $a = v\frac{\mathrm{d}v}{\mathrm{d}x}$ will be undefined and we cannot determine acceleration at that instant with the $v$-$x$ curve.

   Now that actually means that by plotting $v$-$x$ curve we lose information about acceleration of the particle when $v=0$.

I want a method to find the acceleration at that point using $v$-$x$ curve. Also a explanation for this defect of the $v$-$x$ curve.

Also I would like to add that so far no physics book (that I had read) has explained this before writing this relation. Also they do not mention that this will not work for $v=0$.

---

I would like to add the situation where I observed this: when you throw something vertically upward with velocity such that it reaches to a height 10 then the v-x curve will be- 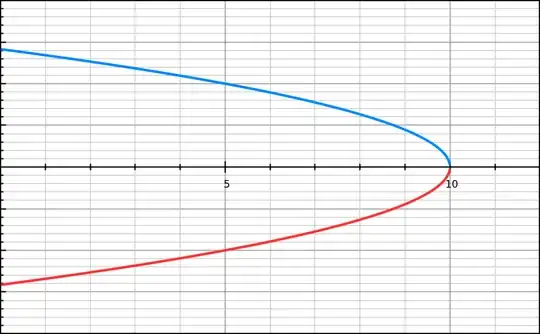the slope of above curve is clearly not defined at x=10(or the instant where velocity is 0) But we know that there was a constant acceleration throughout the flight. Then how can we find acceleration at that instant??? Also assume that we only have v-x curve. Or if we cannot then why??

Answer 1

Your error is simply that you are assuming that $v(x)$ is differentiable with respect to $x$ at $v=0$. The chain rule needs that all derivatives involved exist before you can apply it. In the case of just letting go of something, the function $v(x) = \sqrt{2gx}$ is not differentiable at $x=0$, which is where $v=0$, so you are not allowed to apply the chain rule there.

On the other hand, if $v(x)$ is differentiable where $v=0$, then applying the chain rule is valid. There is nothing fundamental about $v=0$ that prohibits applying the chain rule here, but there is something about your example of letting something fall down that prohibits it.

Lesson: Do not apply rules without checking whether their prerequisites are fulfilled.

Answer 2

When an object starts at rest, the change in velocity when it has made an infinitesimal displacement is infinite - in other words, $\frac{dv}{dx}$ is undefined. You can see this most easily by plotting the curve of $v$ as a function of $x$ for an object starting at rest:

$$x = \frac12 a t^2\\ v = at\\ x = \frac12 a \left(\frac{v}{a}\right)^2\\ v = \sqrt{2ax}$$

When we plot that, we see the slope at $x=0$ is infinite:

And whenever you have "infinite" anywhere in your equations, you need to take the limit. This allows you to find that the expression you have continues to work "right up to" the point where x=0.

Incidentally, I encountered exactly this problem years ago when I was trying to do a numerical integration of an equation of motion - using steps in X, I was unable to get the particle to start moving. Changing to steps in t, the problem goes away...

Answer 3

Consider what you stated:

$$a=v\frac{dv}{dx}$$

Now rewrite it:

$$\frac{dv}{dx}=\frac{a}{v}$$

If $v$ is tiny, then you know that $\frac{dv}{dx}$ must be enormous in order to produce the acceleration that you darn well know exists. Accleration at the top of that trajectory is surely $9.8$ $m/s^2$. As $v$ gets smaller and smaller as it gets to the apex, $\frac{dv}{dx}$ must get larger and larger to preserve the acceleration known to exist. Maybe it will help to think of it as the mathematics is letting you know that an infinity is occurring because a velocity vector reversal is coming very soon. I think that's how you could physically interpret the math. An infinity is coming, and that means a significant physical phenomenon is going to happen. The math is telling us that a vector reversal can happen in time even though the velocity is zero. Time keeps moving forward even though movement reverses.

Answer 4

This equation is best understood in integral form

$$ \left. {\rm d}x = \frac{v}{a}\,{\rm d}v \right\} x_2-x_1 = \int \limits_{v_1}^{v_2} \frac{v}{a}\,{\rm d}v $$

It gives you the distance traveled by a varying acceleration between two speeds. "A car accelerating from 0 to 60 mph needs X distance".

By stating that $v=0$ always not only it implies that $a=0$ (constant acceleration) but also the integration limits are identical $v_1=v_2=0$. As a result the integral is zero and $x_2-x_1 =0 $. This is interpreted as a non-moving body will traverse no distance (duh!).