Physical intuition on the integral contained in d'Alembert's Formula for the wave equation

Question

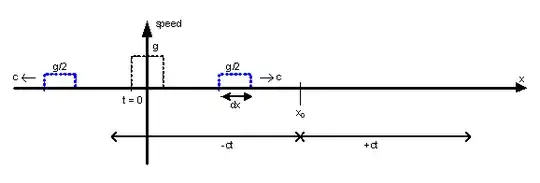
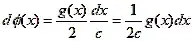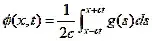If $\phi(t,x)$ is a solution to the one dimensional wave equation and if the initial conditions $\phi(0,x)$ and $\phi_t(0,x)$ are given, then d'Alembert's Formula gives

$$\phi(t,x)= \frac 12[ \phi(0,x-ct)+ \phi(0,x+ct) ]+ \frac1{2c} \int_{x-ct}^{x+ct} \phi_t(0,y)dy . \tag{1}$$

Letting $g(x)=\phi(0,x)$ and $h(x)= \phi_t(0,x)$ (with $c=1$, so $ct=t$) this is commonly written

$$\phi(t,x)= \frac 12[ g(x-t)+ g(x+t) ]+ \frac12 \int_{x-t}^{x+t} h(y)dy . \tag{2}$$

My question:
What is the physically intuitive meaning of the integral term?
For example, why does $\phi_t$ show up in the integral whereas $\phi$ shows up in the forward and backward waves? Why does the integral have those specific limits of integration (and region of integration) for $h$ whereas $g$ uses only the end points, $x+ct,x-ct$? Are there examples with specific functions for $\phi$ that would help to understand this?

References:

http://mathworld.wolfram.com/dAlembertsSolution.html

https://en.wikipedia.org/wiki/D%27Alembert%27s_formula

http://www.jirka.org/diffyqs/htmlver/diffyqsse32.html

http://people.uncw.edu/hermanr/pde1/dAlembert/dAlembert.htm

math.ualberta.ca 337week0405.pdf after equation 180.

stanford univ waveequation3.pdf page 4 Lemma 3 and page 5.

math.nist.gov evolution.pdf page 537

math.usask.ca lamoureax_michael.pdf page 19.

univ. of penn. m425-dalembert-2.pdf first three pages.

univ. of ill. at urbana 286-dalemb.pdf

"Generalized Functions, vol 1", I. M. Gelfand, G. E. Shilov, page 114

"Mathematics for the Physical Sciences", L. Schwartz, pages 253-257

"The Mathematical Theory of Wave Motion", G. R. Baldock, T. Bridgeman, pages 40-45

From these, for example, I know that for a string $\phi_t(0,y)$ represents the velocity at time zero, but why physically (and intuitively) does it end up in the integral. Or I know $(x+ct),(x-ct)$ define the edges of a cone with vertex at $(x,t)$ which form the boundary of the region of the argument of $h$ where $h$ can effect $\phi(t,x)$, but why does the integral have those specific limits of integration for $h$ whereas $g$ uses only the end points, $x+ct,x-ct$?

Answer 1

The D'Alembert solution has a simple interpretation. Using your notation, it reads $$\phi(x, t) = \frac{g(x-t) + g(x+t)}{2} + \frac12 \int_{x-t}^{x+t} h(x') dx'.$$ where $g(x)$ is the initial position, $h(x)$ is the initial velocity, and $v = 1$.

Mathematically, the first term above solves the wave equation with initial position $g(x)$ but zero initial velocity, while the second term does the same for zero initial position and initial velocity $h(x)$. By the superposition principle, their sum has initial position $g(x)$ and initial velocity $h(x)$, and is hence equal to $\phi(x, t)$ for all times.

We can understand each of these individual terms by physical intuition.

First consider the term for initial position $g(x)$. We know all solutions of the wave equation are a linear combination of functions of the form $f(x\pm t)$, so the only things we can use are $g(x+t)$ and $g(x-t)$, which both have the right initial position. Finally, we notice that averaging them produces zero initial velocity by the chain rule. Intuitively, if you hold a string and let go, you will make equal-sized waves going in both directions.

Next consider the term for initial velocity $h(x)$. To understand it, consider the following simpler question: suppose $h(x)$ is zero everywhere except for a sharp spike at $x = 0$, corresponding to us hitting the string there at time $t = 0$. What is the resulting shape?

Physically, we expect a 'shockwave' to propagate outward from this event. Solving the wave equation using a similar technique to the one in the previous paragraph, we find $$y(x, t) = \frac12\left( \theta(x+t) - \theta(x-t) \right).$$ That is, everything inside the "light cone" of $(x, t) = (0, 0)$ has been raised up by $1/2$.

For a general $h(t)$, then, the solution is to integrate this $1/2$ over all light cones that could have affected the point $(x, t)$. The limits of this light cone are $x-t$ and $x+t$, yielding the term $$\frac12 \int_{x-t}^{x+t} h(x') dx'$$ in agreement with the formula.

Answer 2

The following is from https://www.nature.com/articles/s41598-021-99049-7 Supplementary Information Note E

D'Alembert formula integral term physical interpretation and geometric derivation

The figure shows a speed of displacement pulse, g(x,t) initially applied at t = 0 while centered at x = 0, after it has propagated a short time. ( Note that the direction of wave propagation and direction of displacement caused by speed of displacement are not necessarily the same. ) Similarly to a displacement pulse, the speed of displacement pulse has split in two with pulses propagating in both the left and right directions: ½g(x+ct) and ½g(x-ct) .

The resulting displacement at x0 is a function of how long the propagating speed of displacement pulse is applied at x0 as it passes. After the pulse has passed x0 the displacement it caused at x0 persists. This is the reason the displacement at x0 due to an initial speed of displacement depends on the whole interval x0 - ct to x0 + ct. In contrast, the displacement resulting from an initial displacement at t = 0 only exists at the ends of the interval, x0 - ct and x0 + ct. It does not persist at x0 after the pulse passes.

If the spatial length of the pulse is a differential dx then the length of time that the pulse is applied at x0, or any other point, x, that it passes, is dx/c. Since the initial pulse at t = 0 splits into left and right moving pulses the amplitude of the pulse is g(x)/2. The resulting differential displacement is

If the pulse is replaced by an extended function, the resulting displacement would be given by the sum of differential displacements:

where ct is the furthest distance any point on the initial speed of displacement function at t = 0 can reside away from x in either the left or right direction for it to have effect at x at time t.

This is the integral term in D'Alembert's formula [2, 3].

References

1. Bland, D. R. Vibrating Strings 63 (Routledge & Kegan Paul Ltd, London 1960)
2. Borrelli, R. L., Courtney, S. C. Differential Equations (John Wiley & Sons, 1996)
3. Farlow, S. J., Partial differential Equations For Scientists And Engineers (Dover 1993)