Does cutting of trees affect spin angular momentum of earth?

Question

Cutting trees reduces earth's moment of inertia. So the spinning velocity of earth should be reduced day by day. Does it really happen?

Answer 1

Model the tree as a point mass $m$ located some height $h$ above the ground --- that is, forget the mass of the trunk and assume all the mass of the tree is in the branches and leaves above the ground. Then the moments of inertia of the tree before and after felling are \begin{align} I_\text{tree,up} &= m \left( (R+h)\cos\theta \right)^2 \\ I_\text{tree,down} &= m \left( R\cos\theta \right)^2 \end{align} where $R$ is the radius of Earth and $\theta$ the latitude of the tree.

The moment of inertia for the rest of the Earth is $$ I_\text{Earth} \approx \frac25 MR^2 $$ if Earth's mass is $M$ and we pretend Earth is a uniformly-dense sphere. (It isn't, which reduces the fraction out front from $\frac25$ to perhaps something like $\frac15$ --- I haven't done the math carefully or looked it up, and you'll see in a moment it doesn't matter. We'll use the simple assumption.)

Angular momentum is conserved when the tree falls, so the frequency $\omega$ of Earth's rotation changes: $$ (I_\text{up} + I_\text{Earth})\omega_\text{up} = (I_\text{down} + I_\text{Earth})\omega_\text{down} $$ We can figure out how much it changes. Let's fell a tree on the equator, where $\cos\theta=1$, and figure out how much the ratio is: \begin{align} \frac{\omega_\text{down}}{\omega_\text{up}} &= \frac {\frac25M + m(1+\frac hR)^2} {\frac25M + m} \cdot \left(\frac RR\right)^2 \\ &\approx \frac {\frac25M + m + 2m\frac hR} {\frac25M + m} \\ &\approx 1 + 2\frac {m} {\frac25M+m} \cdot \frac hR = 1 + 5\frac{mh}{MR} \end{align} So a six-ton ($m/M = 10^{-20}$), sixty-meter ($h/R = 10^{-5}$) behemoth of a tree on the equator would change the length of a day starting in the 24th significant figure or so. Attoseconds. Felling a big tree would change the length of a day by some attoseconds.

Bigger effects include relative motion of Earth's core and mantle, tectonic shifts, evaporation of equatorial seawater and atmospheric transit of water vapor from tropical to temperate latitude zones or vice-versa. This image 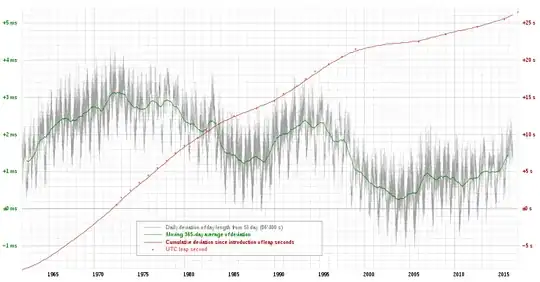suggests there are daily fluctuations in day length of about a millisecond, averaging to about a half-millisecond seasonal variation. That's a seasonal change to the length of a day in the eighth or ninth significant figure.

A fun Fermi problem is to notice there are probably more deciduous trees in the northern than southern hemisphere, and assume they all drop their leaves at once in October; even that is a pretty small change in the length of the day.

Answer 2

I know the example given sounds crazy but the physics behind it might be useful for someone learning rotational dynamics.

The angular momentum of a system does not change if there are no external torques, since $$\frac{d\vec L}{dt}=\vec \tau,$$ where $\vec L$ is the total angular momentum and $\vec \tau$ is the total external torque. So if you cut the trees the angular momentum of the system (Earth+trees) is constant. Leaving the cut trees on Earth does not change the Earth's angular momentum, but since the inertia momentum $I$ has decreased the relation $$L=I\omega,$$ shows that the angular velocity has to increase. The day would be shorter.

On the other hand if you cut and throw them in orbit (just as a didactic example) the trees by themselves might have an arbitrarily given angular momentum. So the Earth's angular momentum would change in order to keep the angular momentum of the system constant.

Answer 3

Cutting the trees and leaving them flat instead of vertical will diminish the moment of inertia of earth. The angular momentum of course will not change, but the speed of rotation will increase. However, I do not believe that the change is measurable with current instruments.

Answer 4

To formalize @knzhou's comment:

The answer, in a nutshell, is no.

Your basic assumption that cutting trees reduces the Earth's mass is wrong, because trees don't leave the Earth when they are cut!

Even if all trees left the Earth when cut,

1. a lot of tree cutters plant trees to replace what they cut, and
2. each tree is such a tiny amount of mass compared to Earth's mass that it doesn't really affect anything.

Hope this helps!

@Rob's calculations are the best place to look for a better explanation.

Answer 5

You might hear the story about figure skating. When a rotating person expands his/her arm, he/she can slow down rotation. Same thing can happen with earth. Assuming the tree is trillion tons and you cut it and lift it up, you can slow down the earth.

Answer 6

I would think that the whole atmosphere surrounding the earth is far heavier than the trees that were cut. The atmosphere turns with the earth and the changed position of trees would not even be noticed.

Answer 7

Displacing some mass closer to the axis of rotation reduces the moment of inertia $I$. Considering Earth as an isolated system (which is not), its angular momentum $L$ must be conserved:

$$L=I\omega = \text{const}$$

Therefore if $I$ goes down, the rotation frequency $\omega$ must increase. But if we should also consider the reduction of $I$ while the tree was growing, displacing mass away from the axis of rotation, so by cutting a tree to the ground we are simply bringing back $\omega$ to the value it had before the tree was born.

If the average number of trees is going down, then this contributes to speed up the Earth's rotation. By how much? A tiny amount hidden into a bunch of stronger perturbations which still are really weak.