Friction to just move the blocks

Question

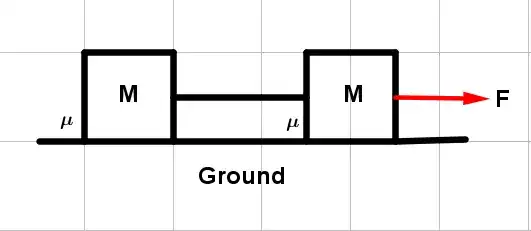
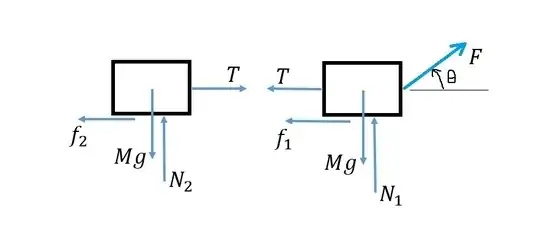
Two blocks each of mass $m$ are placed on a rough horizontal surface and connected by mass-less in-extensible string as shown.The coefficient of friction between each block and ground is $\mu$ What would be the minimum force $F$ to be applied on the right hand side block to move the block system horizontally without letting the string getting slack.

Now I thought of a simple thing that maximum $$\sum F_{right direction}=F$$ $$\sum F_{left direction}=2\mu mg$$

And hence to just move the block system I need $$F=2\mu mg$$

But my answer is wrong which in turn in $$F=\frac{2\mu mg}{\sqrt{1+\mu^2}}$$

Can anybody give me a hint, where I went wrong.

Answer 1

The original problem wants to find minimum force to move horizontally and this doesn't mean that force $F$ should necessarily be horizontal. We have: $$N_1=Mg-F\sin\theta\;\tag 1$$ $$F\cos\theta-T-f_1=0\;\tag 2$$ $$T-f_2=0\;\tag 3$$ $$N_2=Mg\;\tag 4$$ Because of the condition of verge of motion, we have: $$f_1=\mu N_1\;\tag 5$$ $$f_2=\mu N_2\;\tag 6$$ Then, we obtain: $$F=\large{\frac{2\mu Mg}{\cos\theta+\mu\sin\theta}}$$ For minimizing $F$, it should be: $$\large{\frac{\partial F}{\partial\theta}}=0$$ So, it is obtained that: $$\mu=\tan\theta$$ Finally, we reach to the desired answer: $$F_{\textrm{min}}=\frac{2\mu Mg}{\sqrt{1+\mu^2}}$$

Answer 2

As you only asked for a hint, not an answer:

Your answer is coming just by considering the force F to be horizontal. But what if it's not horizontal or what if it have a vertical component too? This vertical component will decrease the normal on the right block, so it will also decrease friction.

For minimum force, assume the force to be at some angle, make the equations, differentiate it to get the minimum force, and you will get a particular angle. And for that angle get the force.