Why is the Sun called an "average star"?

Question

This is a statement (presumably in mass, longevity, energy output) many people that I've met have heard in school, and it is known in pop culture. However, according to Wikipedia, about 75% of the stars in the universe are red dwarfs, which greatly differ from the sun. I've tried doing a little bit of research and I've found that the sun is "average" if you exclude all the dwarf stars from you calculations. Is there a good reason why this is done?

Answer 1

Describing the sun as an average star is probably more of a reaction against the idea that there is something unique about it. Obviously there is for us, since it is the star that we happen to be in orbit around, and much closer to than any other star, and hence historically the sun has been considered rather unique. But over the centuries we've discovered that neither the sun nor the earth is the center of the universe, that the stars we see in the night sky are just like our own sun, and that some of them are much brighter and/or much larger (in mass or volume).

So saying the sun is an average star is mostly a historical artifact. It is saying that we've discovered that there is nothing particularly unusual about our star compared to any other star in our galaxy.

It isn't a claim that the sun is average in any particular mathematical sense. It is using 'average' in the sense of 'typical' or 'unexceptional'. As it happens, it turns out the majority of stars are in fact smaller and less luminous than our sun, so it is somewhat un-average in that sense.

Answer 2

Why is the Sun called an “average star”?

The sun is a yellow dwarf star and dwarf stars are the most common in the universe. Technically, the sun's spectrum peaks in the range of green light, but we see it as effectively white.

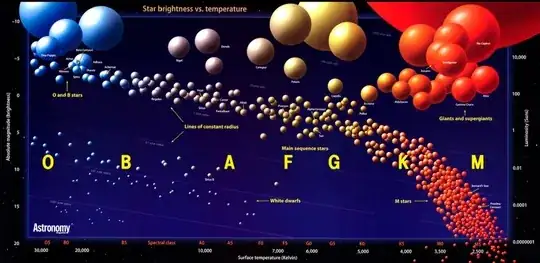
I am inclined to think if an astronomer or physicist told you the sun was "average" it is because it is part of the main sequence line of the Hertzsprung–Russell diagram (see below).

Most of the stars on this line are classified as dwarf stars.

...about 75% of the stars in the universe are red dwarfs, which greatly differ from the sun.

I am not sure greatly is the best word. Yes red dwarfs are generally cooler, less massive, and their interiors dominated by convection, but by appearance alone their differences are not all that great.

I've tried doing a little bit of research and I've found that the sun is "average" if you exclude all the dwarf stars from you calculations.

By all the dwarf stars do you mean orange, yellow, red, white, and brown dwarfs, etc.? If you eliminate all of these except for the sun, then the sun would be extremely odd.

Is there a good reason why this is done?

I am not sure what you did exactly, but I think you may have misunderstood what was meant by "average" (see my comments above).

Answer 3

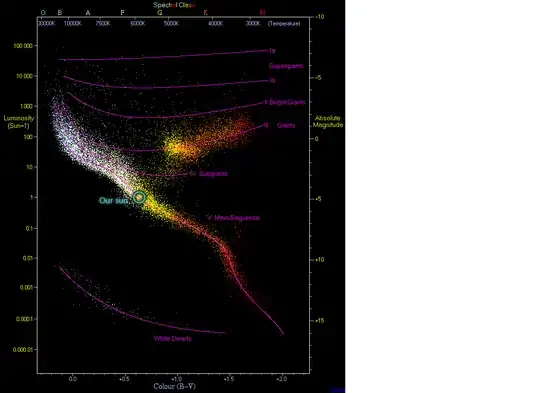
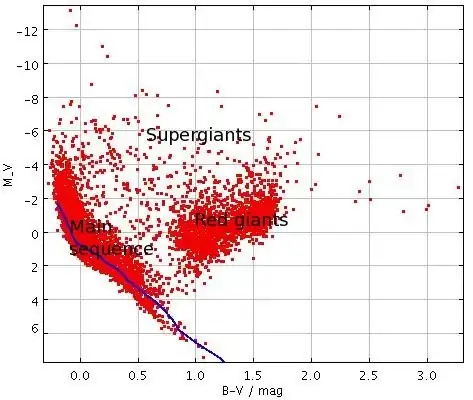
As a followup to @honeste_vivere's note about the H-R diagram, our sun really is living in the middle of average-town:

The image, from Wikipedia plots 22,000 stars. When you plot a star's temperature vs brightness, they seem to follow certain patterns.

Our star lies right in the middle of the boring main sequence.

Answer 4

The Sun is decidedly NOT an average star, except that it is on the hydrogen-burning main sequence, where $\sim 90$% of stars in the local stellar population are found.

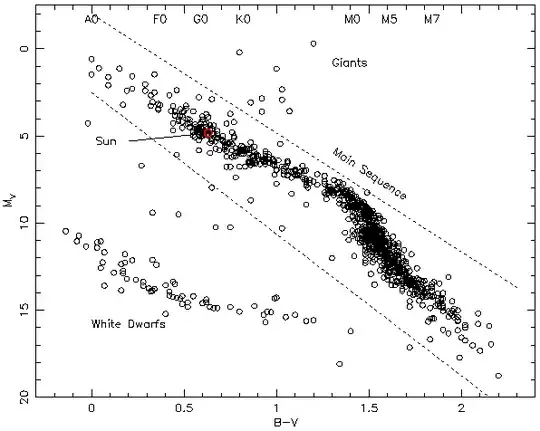
A much better appreciation of the Sun's "un-averageness" is gained from looking at a Hertzsprung-Russell diagram (luminosity vs effective temperature or equivalently, absolute magnitude versus colour) of stars in a volume limited sample around the Sun. This is far more representative of a stellar population than looking at a brightness-limited sample.

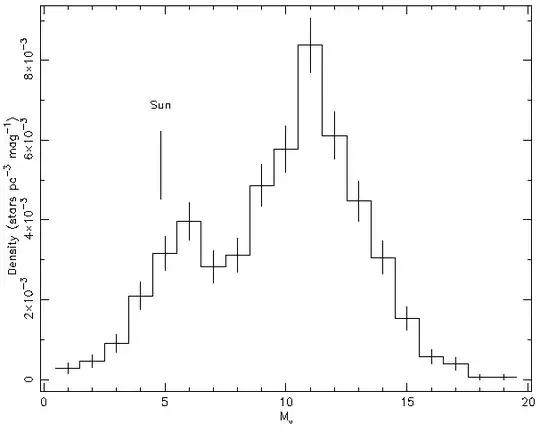
Below I show the volume limited colour versus absolute magnitude diagram that I derived (see Jeffries & Elliott 2003 - a paper that sets out to answer exactly this question) from the closest 1000 stars to the Sun, taken from the Gliese & Jahreiss (1991) third catalogue of nearby stars. I have added spectral types and show the location of the Sun in such a diagram. Below that, I show a frequency histogram of main sequence stars (a so-called "luminosity function"), that shows where the Sun lies with respect to the local population.

You can see from this that the Sun is in the highly populated main sequence band, but it is actually more luminous (and more massive) than 88% of stars on the main sequence. A median star on the main sequence has an absolute visual magnitude of $\sim 11$, is about 100 times less luminous than the Sun (300 times fainter in terms of its absolute visual magnitude) and has a mass of around $0.3M_{\odot}$. In fact, even the sample I show below is not complete and over the last couple of decades, even more examples of faint stars and brown dwarfs have now been found.

The reason that people think that the Sun is "average" is because of diagrams like those in the wikipedia page (as seen in Ian Boyd's answer). This conflates HR diagrams of both the local population and with a magnitude-limited sample which overly emphasises the populations of very luminous main sequence stars and red giants, which are in fact very rare.

Compare the above HR diagram with that below, which is constructed by taking Hipparcos parallaxes for all the stars that can be seen with the naked eye (those with $V<6$). The Sun would be right at the bottom of this diagram - there are no "typical" (modal) stars visible to the naked eye.

Answer 5

As I mentioned in first comment underneath original question, the Hertzsprung-Russell diagram is probably the single best measure of "average" if you have to choose just one measure. But since there seem to be many more additional answers and comments than I'd assumed would be posted, let me add the following remarks that seem to have been overlooked.

In terms of stellar evolution, the entire life history of a star can be predicted from just three parameters: its initial mass, its initial chemical composition, and its initial angular momentum. That's it. So if you want to quantitatively discuss "average", it's these three things you should be talking about.

But since there are lots of relations, e.g., the mass-luminosity relation, you can boil the whole mess down to the Hertzsprung-Russell diagram if you don't need to be too quantitative.

And I'd also note what seems to be a pretty ubiquitous blunder in the above remarks that the sun isn't "average luminosity" because there are many more stars that are less luminous. That's quite true, but what it means is that the sun isn't >>median<< luminosity. For >>average<<, you'd want to take the galaxy's total luminosity and divide by $\sim2.5\times10^{11}$ (#stars in milky way). So, the galaxy's energy output is $\sim5\times10^{37}\mbox{watts}$, and the sun's is $\sim3.85\times10^{26}\mbox{watts}$. Pretty darn close to average.