8

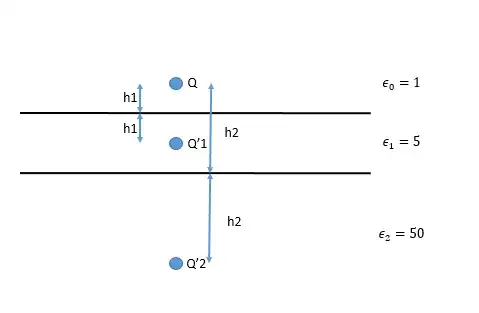
If I have a charge $Q$ located over a 2 layer dielectric as represented: imagemethod2layers

According to the image method: the charge $Q'1$ will be located at a distance $h_1$ under the first interface and the $Q'2$ will be located at a distance $h_2$ under the first interface.

With:

$$ Q'1 = \frac{\epsilon_0-\epsilon_1}{\epsilon_0+\epsilon_1} = \frac{1-5}{1+5} Q $$

My problem is determining the value of $Q'2$, is it: $$ Q'2 = \frac{\epsilon_1-\epsilon_2}{\epsilon_1+\epsilon_2} = \frac{5-100}{5+100} Q $$

or

$$ Q'2 = \frac{\epsilon_0-\epsilon_2}{\epsilon_0+\epsilon_2}= \frac{1-100}{1+100} Q $$

Urb
  • 2,724
Anthony Lethuillier
  • 293

1 Answers1

2

From Jackson's Electrodynamics: the potential in the $\epsilon_1$ region for a single interface is as if there is an image charge $Q''=\frac{2\epsilon_1}{\epsilon_1+\epsilon_0}Q$ at the position of $Q$. Therefore the correct $Q'2$ is

$$Q''\frac{\epsilon_1-\epsilon_2}{\epsilon_1+\epsilon_2}=\frac{2\epsilon_1}{\epsilon_1+\epsilon_0}\frac{\epsilon_1-\epsilon_2}{\epsilon_1+\epsilon_2}Q$$

which seems to have the right behavior in the two limiting cases $\epsilon_0=\epsilon_1$ and $\epsilon_1=\epsilon_2$.

fferen
  • 247