I am looking at Jackson sec 11.9, where he states that the $\rho,\bf{J}$ form the 4-current $$J^\alpha=(c\rho,\bf{J})$$ Jackson says this is from the invariant of the 4-divergence $\partial^\alpha J_\alpha$ is invariant (which is 0 for the 4-current).
So I want to understand this in terms of a point charge, where $$\rho= q\delta^3({\bf r}-{\bf r}(t))$$ $${\bf J} = q{\bf v}(t)\delta^3({\bf r}-{\bf r}(t))$$ Is there a way to understand why this transforms as a 4-vector?
As per, http://en.wikipedia.org/wiki/Four-velocity, we can define four-current density as: $J = \rho_0 U$, where $U$ is the four-velocity. Since it's a scalar times a four-vector, it's another four-vector.
$$J = \gamma(v)(\rho_0 c,\rho_0 \vec{v})$$ $$J = (\gamma(v)\rho_0 c,\gamma(v)\rho_0 \vec{v})$$
Now it remains to show that this fits the definition you gave:
$$J=(c\rho,\mathbf{J})$$
ie: We need to show that $$\rho = \gamma(v)\rho_0$$ $$\mathbf{J} = \gamma(v)\rho_0 \vec{v}=\rho \vec{v}$$
Suppose we have an infinitesimal volume of charge moving with velocity $\vec{v}$. Suppose its dimensions in the rest frame are $\Delta x'$,$\Delta y'$, $\Delta z'$. Its volume in the rest frame $V' = \Delta x'\Delta y'\Delta z'$. Total charge within this volume is $\rho_0V'$. We know by length contraction that $\Delta x = \dfrac{\Delta x'}{\gamma(v)}$, $\Delta y = \Delta y'$, $\Delta z = \Delta z'$.
So in the original frame the volume of this charge is: $V = \Delta x \Delta y \Delta z = \dfrac{V'}{\gamma(v)}$.
Total charge is the same in both frames (why? we define charge as being measured in the rest frame, making it invariant).
So charge density in original frame, $\rho = \dfrac{\rho_0 V'}{\left(\dfrac{V'}{\gamma(v)}\right)} = \gamma (v)\rho_0 $
so that takes care of the first relation. The second relation $$\mathbf{J} = \rho \vec{v}$$ just follows from the definition of current density. Going back to our infinitesimal volume of charge, suppose the charge crosses some boundary perpendicular to the x-axis over some time $\Delta t$. $$I = \dfrac{Q}{\Delta t} = \dfrac{\rho \Delta x \Delta y \Delta z}{\Delta t}$$ Cross sectional area $$A = \Delta y \Delta z$$ So magnitude of current density = $\dfrac{I}{A} = \dfrac{\rho \Delta x}{\Delta t}$. Taking infintesimals we get $\rho \left|\left|\dfrac{dx}{dt}\right|\right|$. Multiply this by a unit vector in the direction of motion and we get $$\mathbf{J} = \rho \vec{v}$$
I use other symbols in order to prevent confusion in the following.
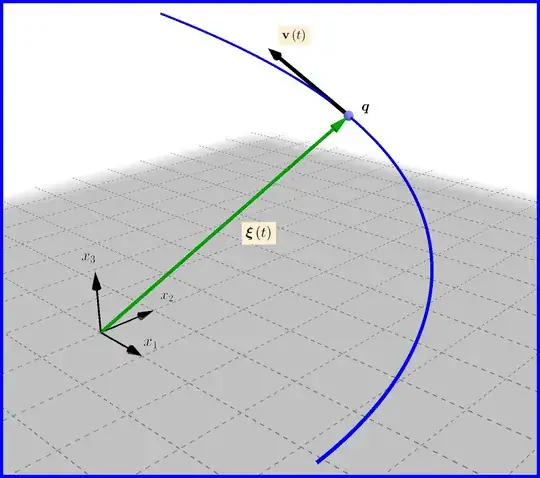
Let a point charge $\:q\:$ moving with position vector $\:\boldsymbol{\xi}\left(t\right)\:$ as in above Figure. Then the volume charge density and the charge current density are expressed via Dirac $\:\delta$-function as follows
\begin{align} \rho\left(\mathbf{x},t\right) & =q\cdot\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \tag{01a}\\ \mathbf{j}\left(\mathbf{x},t\right) & =q\cdot\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \cdot\dfrac{d\boldsymbol{\xi}\left(t\right)}{dt}=q\cdot\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot\mathbf{v}\left(t\right) \tag{01b} \end{align} where \begin{equation} \mathbf{v}\left(t\right)= \bigl(\upsilon_{1}\left(t\right),\upsilon_{2}\left(t\right),\upsilon_{3}\left(t\right)\bigr)= \biggl(\dfrac{d\xi_{1}\left(t\right)}{dt},\dfrac{d\xi_{2}\left(t\right)}{dt},\dfrac{d\xi_{3}\left(t\right)}{dt}\biggr)= \dfrac{d\boldsymbol{\xi}\left(t\right)}{dt} \tag{02} \end{equation} the velocity of the charge. Under the assumption that the electric charge $\:q\:$ is invariant (observers in different inertial systems agree on the same value) we must show that the 4-quantity \begin{equation} \dfrac{\mathbb{J}}{q} \equiv \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr), \:\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot\dfrac{d\boldsymbol{\xi}\left(t\right)}{dt} \right] \tag{03} \end{equation} is a 4-current. So we must prove that it satisfies the continuity equation \begin{equation} \dfrac{\partial \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \right]}{\partial t}+ \boldsymbol{\nabla}_{\mathbf{x}}\boldsymbol{\cdot} \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot\dfrac{d\boldsymbol{\xi}\left(t\right)}{dt} \right]=0 \tag{04} \end{equation} or \begin{equation} \dfrac{\partial \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \right]}{\partial t}+ \boldsymbol{\nabla}_{\mathbf{x}}\boldsymbol{\cdot} \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot\mathbf{v}\left(t\right)\right]=0 \tag{04a} \end{equation} If proved, this 4-current would be a 4-vector also.
Now \begin{equation} \delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) =\delta\bigl(x_{1}-\xi_{1}\left(t\right)\bigr)\cdot\delta\bigl(x_{2}-\xi_{2}\left(t\right)\bigr)\cdot\delta\bigl(x_{3}-\xi_{3}\left(t\right)\bigr) \tag{05} \end{equation} Using the following property of Dirac $\:\delta$-function \begin{equation} z\delta\left( z \right)=0 \Rightarrow \dfrac{\partial \delta\left(z\right)}{\partial z} = - \dfrac{ \delta\left(z\right)}{ z} \tag{06} \end{equation} we have \begin{equation} \dfrac{\partial \left[\delta\bigl(x_{k}-\xi_{k}\left(t\right)\bigr) \right]}{\partial t}=\:+\:\dfrac {\dfrac{d \xi_{k}}{dt}}{x_{k}-\xi_{k}\left(t\right)}\cdot\delta\bigl(x_{k}-\xi_{k}\left(t\right)\bigr)=\:+\:\dfrac {v_{k}\left(t\right)}{x_{k}-\xi_{k}\left(t\right)}\cdot\delta\bigl(x_{k}-\xi_{k}\left(t\right)\bigr) \tag{07} \end{equation}
So \begin{equation} \dfrac{\partial \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \right]}{\partial t}=\:+\left(\sum_{k=1}^{k=3}\dfrac {v_{k}\left(t\right)}{x_{k}-\xi_{k}\left(t\right)}\right)\cdot\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \tag{08} \end{equation} On the same footing we can prove that \begin{equation} \dfrac{\partial \left[\delta\bigl(x_{k}-\xi_{k}\left(t\right)\bigr)\cdot v_{k}\left(t\right)\right]}{\partial x_{k}}=\:-\:\dfrac {v_{k}\left(t\right)}{x_{k}-\xi_{k}\left(t\right)}\cdot\delta\bigl(x_{k}-\xi_{k}\left(t\right)\bigr) \tag{09} \end{equation} that is \begin{equation} \boldsymbol{\nabla}_{\mathbf{x}}\boldsymbol{\cdot} \left[\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot\mathbf{v}\left(t\right)\right]=\:-\left(\sum_{k=1}^{k=3}\dfrac {v_{k}\left(t\right)}{x_{k}-\xi_{k}\left(t\right)}\right)\cdot\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) \tag{10} \end{equation} proving the continuity equation (04).
EDIT : A strange invariant
Realizing that the 4-quantity $\left(\mathbb{J} /\right)q$ of equation (03) is a contravariant 4-vector, say $\mathbb{V}$
\begin{equation}
\mathbb{V} \equiv \delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot \left[c, \:\dfrac{d\boldsymbol{\xi}\left(t\right)}{dt} \right]=\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)\cdot\Biggl[\:\:c\:\:,\:\:\mathbf{v}\:\:\Biggr]
\tag{11}
\end{equation}
and having in mind- (and comparing it with-) the contravariant 4-vector for velocity
\begin{equation}
\mathbb{U} \equiv \gamma_{v}\cdot \left[c, \:\dfrac{d\boldsymbol{\xi}\left(t\right)}{dt} \right]=\gamma_{v}\cdot\Biggl[\:\:c\:\:,\:\:\mathbf{v}\:\:\Biggr]
\tag{12}
\end{equation}
I was wondering which would be the relation between the Dirac $\:\delta$-function $\delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr)$, a function of $\:\left(\mathbf{x},\:t\:\right)$, and $\:\gamma_{v}\:$, a function of $\:t\:$
\begin{equation}
\gamma_{v}= \left[1-\left(\dfrac{v}{c}\right)^{2}\right]^{-1/2}=\left[1-\left\Vert\dfrac{d\boldsymbol{\xi}\left(t\right)}{c dt}\right\Vert ^{2}\right]^{-1/2}
\tag{13}
\end{equation}
We know that the inner product of two 4-vectors (in Minkowski space) is Lorentz-invariant, so
\begin{equation}
\mathbb{U}\boldsymbol{\circ} \mathbb{V }= c^{2}\left[1-\left\Vert\dfrac{d\boldsymbol{\xi}\left(t\right)}{c dt}\right\Vert ^{2}\right]^{1/2}\cdot \delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) = \text{invariant}
\tag{14}
\end{equation}
If we see this invariant in the rest frame of the particle, then
\begin{equation}
\bbox[#FFFF88,12px]{\left[1-\left\Vert\dfrac{d\boldsymbol{\xi}\left(t\right)}{c dt}\right\Vert ^{2}\right]^{1/2}\cdot \delta^{3}\bigl(\mathbf{x}-\boldsymbol{\xi}\left(t\right)\bigr) = \text{invariant}=\delta^{3}\bigl(\mathbf{x}_{rf}\bigr)}
\tag{15}
\end{equation}
where $\:\mathbf{x}_{rf}\:$ the position vector of a reference point with respect to the rest frame of the particle.
$=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!=\!$
$\:\color{red}{\textbf{THIS ANSWER OF MINE IS WRONG !!!}}$ because
Proofs that the 4-dimensional electric charge current density $\,\mathbf J\,$ is transformed as a Lorentz 4-vector based upon the conservation law (continuity equation) are false. That electric charge is constant in an inertial system doesn't provide any information about how it is transformed between inertial systems. It's a confusion between what is a constant (it concerns what happens in a system) and what is an invariant (it concerns what happens between two systems).
\begin{equation} \partial_{\mu}A^{\mu}\boldsymbol{=}\texttt{invariant}\quad \boldsymbol{=\!\ne\!\Rightarrow}\quad A^{\mu}\boldsymbol{=}\texttt{contravariant Lorentz 4-vector} \tag{16}\label{16} \end{equation}
Here is a quick (standard) proof of the quotient rule in the context of the four-current being Lorentz covariant, as mentioned by @SebastianRiese. We assume that in any inertial frame (where the metric is Minkowski, as expressed in the coordinates we are using) the physical continuity equation holds:
$$\frac{\partial\rho}{\partial t}+\nabla\cdot \vec{J}=0\tag{1}$$
Knowing that the partial derivatives $\partial_{\mu}$ do transform as Lorentz vectors, we write the continuity equation in a suggestive form.
$$\partial_{\mu}J^{\mu}=0 \tag{2}$$
where as usual I have defined:
$$\partial_{\mu}\equiv \frac{\partial}{\partial x^{\mu}}=\left(\frac{\partial}{\partial (ct)},\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\tag{3}$$
$$J^{\mu}=\begin{pmatrix}c\rho\\ J^x\\J^y\\J^z\end{pmatrix}\tag{4}$$
What is important to remember here is that although we know how the derivative four-vector changes under general coordinate transformations (among them Lorentz transformations), we do not yet know how this four-component $J^{\mu}$ changes under coordinate transformations - i.e. we do not really know if it is actually a four-vector. We do know that under general under rotations $\vec{J}$ will physically transform as a Cartesian vector and $\rho$ a Cartesian scalar, but it is not immediately obvious that under boosts $\vec{J}$ and $\rho$ will mix as they would if they were unified into the four-vector $J^{\mu}$ from (4).
The trick is to realize that on the RHS of eq. (2), we have $0$ which is a Lorentz scalar. Lorentz transform to another inertial coordinate system, where the continuity equation is now:
$$\begin{align} \partial'_{\mu}J'^{\mu}&=\left(\Lambda_{\mu}^{\,\,\nu} \partial_{\nu}\right)J'^{\mu}\\ &=\partial_{\nu}\left(\Lambda_{\mu}^{\,\,\nu}J'^{\mu}\right)\\ &=\partial_{\nu}J^{\nu}\\ &=0 \end{align}$$
where in passing from the first line to the second I have used that Lorentz transformations are constant in coordinates. This implies the transformation rule for $J^{\mu}$:
$$J'^{\mu}=\Lambda_{\nu}^{\,\,\mu}J^{\nu}=\Lambda^{\mu}_{\,\,\nu}J^{\nu}\tag{5}$$
So the 4-current is indeed a Lorentz vector.
