8

I want to understand what the reciprocal lattice is and how it is connected to the Ewald sphere.

I know a very similar question has been asked on this site already: Reciprocal lattices. The top answer states:

...The reciprocal lattice is simply the dual of the original lattice. And the dual lattice has a simple visual algorithm.

  1. Given a lattice $L$, for each unit cell of $L$ find the point corresponding to that cell's "center of mass" (see below).

  2. Connect each such "center of mass" to its nearest neighbors.

  3. The resulting lattice is the dual of $L$.

Another explanation of the reciprocal space comes from Ashcroft/Mermin Solid State Physics. On page 86 the authors define the reciprocal lattice as follows:

The set of all wave vectors $\mathbf K$ that yield plane waves with the periodicity of a given Bravais lattice is known as its reciprocal lattice.

This is very confusing. The first answer seems to suggest that the reciprocal space is some sort of useful abstract geometrical construction while the definition from Ashcroft and Mermin seems to imply that the reciprocal space actually results from a physical phenomenon (Diffraction). Which one of them is correct?

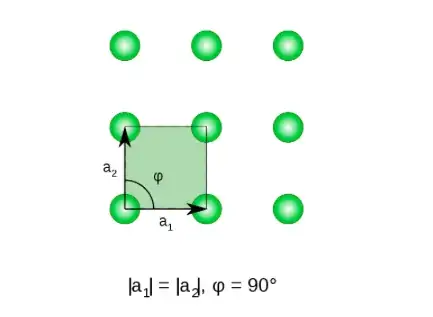
Let's suppose I shoot some x-rays at this Bravais lattice: (Source: Wikipedia)

enter image description here

According to the Bragg formulation of x-ray diffraction, for the rays to interfere constructively, the path difference must be an integral number of wavelengths:

$$n \lambda =2d \sin{\theta}$$

Why is perfect constructive interference necessary? Isn't it enough to demand that there shouldn't be perfect destructive interference?

Assume I rotate a detector and an emitter around my crystal. Are the diffraction patterns that I see on my detector the reciprocal lattice? How is the reciprocal lattice linked to the Ewald sphere? Why do we even need to construct the Ewald sphere?

I know this is a long question but I really would like to understand this.

Community
  • 1
qmd
  • 899

1 Answers1

4

Both descriptions are correct; some people prefer the geometric description: the lattice of atoms is replace by a collection of planes, with different orientations. This corresponds to the Bragg model of partially reflective mirrors, and the K-vectors give the directions for the reflections which form the diffraction pattern.

The description given by Ashcroft & Mermin simply puts the diffracted waves first, and the planes follow. Since it is the waves that one measures, this is more physical to some experimentalists.

However, if you actually work with crystals, the abstract planes from the geometric definition correspond to the cleavage planes.

The Bragg formula gives the paths of constructive interference; these are the bright spots in the diffraction pattern. You could also find the dark places, but the usual thing is to map out the bright spots, as this is sufficient to determine the crystal structure.

The Ewald sphere is a map of the reciprocal lattice, and corresponds to rotations as you describe. For x-rays it is a valuable tool, for it tells you which spots are accessible. With electron diffraction the wavelengths are so short that essentially all of the diffraction spots are accessible at once.

Powder diffraction provides an average across all of the rotations, because the powder already contains all of the possible orientations simultaneously.

Ewald sphere tutorial.

Peter Diehr
  • 7,367