How can an electron fake a jet?

Question

This is a question for experimentalists. I have seen in several ATLAS papers (see for example chapter 4 in arXiv:1602.09058, 6th paragraph), that after objects have been correctly identified, any jet close enough to a candidate electron is removed from the event. The reason seems to be that real electrons can fake a jet, so they simply remove all jets within $\Delta R=0.2$ from the electron in order to avoid double counting (and maybe loosing the electron after imposing isolation requirement?).

My question is how can an electron fake a jet? I am not an experimentalist and for me the detector environment looks something like this:

An electron is one track in the tracker that then becomes a smeared blob in the ECAL. On the other hand, jets are a bundle of nearby tracks (if charged) in the silicon tracker followed by a blob in the ECAL and a bigger blob in the HCAL. So how can an electron be mistaken for a jet if they are near by? The other way around makes more sense to me (an electron faked by a jet). Can electrons puncture into the HCAL?

Answer 1

Hadronic jets deposit a significant fraction of their energy in the electromagnetic calorimeter, for example because they can contain neutral pions that decay as $\pi^0\to\gamma\gamma$, bottom/charm mesons with semi-leptonic decays... Therefore the jet reconstruction algorithm uses energy deposits from both electromagnetic and hadronic calorimeters, so that the jet four-momentum can be estimated as precisely as possible.

This is why an electron is most of the time also reconstructed as a jet: it leaves all (most of) its energy in the EM calorimeter, and this energy deposit is used by the jet reconstruction algorithm.

So, from a genuine electron signal, one ends up typically with two reconstructed objects: an electron and a jet. Double-counting is not what we want, so the typical overlap removal procedure described in ATLAS papers is used to chose which object should be kept - and the other is discarded.

Answer 2

Those of us who've worked at JLAB (and those who worked at SLAC) know that energetic electrons create a lot of hadronic junk when incident on significant amounts of matter. Think about Deep Inelastic Scattering.

Once you have an electron with energy in the few GeV range or higher there is a significant chance of creating pions or other light mesons in the ECAL with non-trivial kinetic energy themselves. These will be mostly forward going, so pointed toward the HCAL.

What I don't know is how often there are electrons in that energy range, but I think they could be pretty common.

Answer 3

Edit: I am leaving this in because some effort has been made to present how decisions are made on complicated channels.The simple answer by @atlas-insider clarifies the general point that the OP is asking.

From the sample ATLAS paper given in the comments

Search for supersymmetry at $\sqrt{s}=13\ \rm TeV$ in final states with jets and two same-sign leptons or three leptons with the ATLAS detector

A search for strongly produced supersymmetric particles is conducted using signatures involving multiple energetic jets and either two isolated leptons ($e$ or $\mu$) with the same electric charge or at least three isolated leptons. The search also utilises $b$-tagged jets, missing transverse momentum and other observables to extend its sensitivity. The analysis uses a data sample of proton-proton collisions at $\sqrt{s}=13\ \rm TeV$ recorded with the ATLAS detector at the Large Hadron Collider in 2015 corresponding to a total integrated luminosity of $3.2\ \rm fb^ {-1}$.

one sees that this is a specific search which needs as a signature jets and leptons.

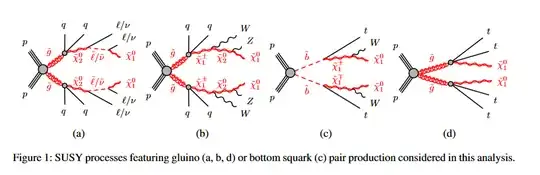
Monte Carlo simulations are used extensively to find the probability of misidentification of candidates due to jets coming from backround reactions to the one sought and the posibility of the leptons coming from decays of unwanted, as far as the channel under study, channels.

After object identification, overlaps between objects are resolved. Any jet withing a distance $\Delta R_y=\sqrt{(\Delta y)^2+(\Delta\phi)^2}=0.2$ of an electron candidate is discarded, unless the jet has a value of the $\rm MV2c20$ discriminant larger than the value corresponding to approximately an $80$% $b$-tagging efficiency, in which case the electron is discarded since it is likely originating from a semileptonic $b$-hadron decay. Any remaining electron within $\Delta R_y=0.4$ of a jet is discarded. Muons within $\Delta R_y=0.4$ of a jet are also removed. However, if the jet has fewer than three associated tracks, the muon is kept and the jet is discarded instead to avoid inefficiencies for high-energy muons undergoing significant energy loss in the calorimeter.

In this particular search there are gauges on deciding when one has a candidate supersymmetric event, which have been decided from a Monte Carlo simulation of the desired events in the detector. Jets or electrons are rejected if the probability they are coming from a background is high.

Signal electrons must satisfy a tight likelihood-based identification requirement [57, 58] and have $|\eta|<2$ to reduce the impact of electron charge mis-identification. Signal muons must fulfil the requirement of $|d_0|/\sigma(d_0)<3$. The track associated to the signal leptons must have a logitudional impact parameter with respect to the reconstructed primary vertex, $z_0$, satisfying $|z_0\sin\theta|<0.5\ \rm mm$. Isolation requirements are applied to both the signal electrons and muons. The scalar sum of the $p_{\rm T}$. The track isolation cone radius for electrons (muons) $\Delta R_\eta=\sqrt{(\Delta\eta)^2+(\Delta\phi)^2}$ is given by the smaller of $\Delta R_\eta=10\ {\rm GeV}/p_{\rm T}$ and $\Delta R_\eta=0.2(0.3)$, that is, a cone of size $0.2(0.3)$ at low $p_{\rm T}$ but narrower for high-$p_{\rm T}$ leptons. In addition, in the case of electrons the energy of calorimeter energy clusters in a cone of $\Delta R_\eta=0.2$ around the electron (excluding the deposition from the electron itself) must be less than $6$% of the electron $p_{\rm T}$. Simulated events are corrected to account for minor differences in the lepton trigger, reconstruction and identification efficiencies between data and MC simulation.

The end result is the possibility of setting a limit for the discovery of the supersymmetric channel being studied.

The acceptance or rejection of a lepton or a jet for the definition of the topology of the reactions studied, in this case looking for supersymmetric signals, depends crucially on the specific channel. It depends on studying the mathematics of the expected kinematics from the channels under study.

It may be that one finds some standard numbers for rejection, this is due to the fact that the detector's accuracies have been studied with similar Monte Carlo tools, but still it is not general rejection without carefully studying the distributions for each channel under study.

So it is not that the electron can fake a jet, as jets start together with the electron track in the tracking detectors. It can be an electron from an unwanted jet or lepton from b or lower resonance decays, for example. The same is true for jets. One searches for the jet and lepton topologies shown in the copied figure on top, and develops rejection measures appropriate for the channels .