1

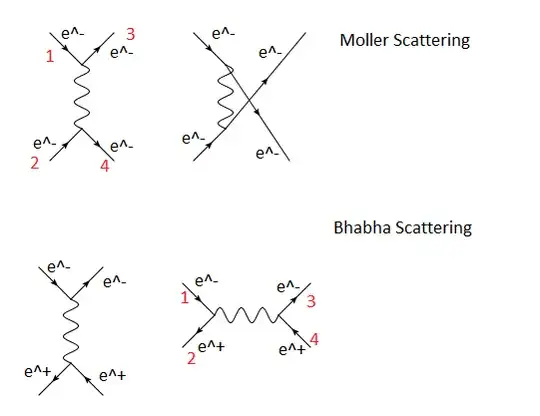
Given the amplitude for a particular process, it may be possible to obtain the amplitude for another similar process by a so called crossing symmetry. I know there is a $s \leftrightarrow u$ crossing symmetry between the tree level diagrams appearing in Bhabha ($e^+ e^- \rightarrow e^+ e^-$) and Moller scattering ($e^- e^- \rightarrow e^- e^-)$ However, I am trying to understand how this is obtained. I put the relevant diagrams in the picture below.

enter image description here

What I have been trying to do is rotate the $s$ channel diagram appearing in Bhabha scattering (bottom right) to get a $t$ channel diagram with which I can relate to the $t$ channel diagram already appearing in the Moller scattering (top left). This would imply $p_1 \rightarrow p_1,\,\, p_2 \rightarrow -p_4, \,\,p_3 \rightarrow -p_2,\,\, p_4 \rightarrow p_3$ but this does not give the $s \leftrightarrow u$ sought after.

Thanks for any explanations!

CAF
  • 3,649

1 Answers1

2

Crossing symmetry tells you that you should not only exchange $$p_2\leftrightarrow -p_4$$ in the amputated matrix elements, but also replace the wavefunction polarizations $$ u^{\pm}(p_2)\rightarrow v^{\mp}(p_4) $$ (where the spin polarizations have been reversed), and finally multiply the amplitude for a factor $-1$ (Since you are crossing a fermionic pair).

All of this is equivalent to the simple $s\leftrightarrow u$ only for the forward scattering at $t=0$ or for the scattering averaged over all the polarizations.

TwoBs
  • 5,222