0

I have two questions about Magnetic Field.

  1. Given a particle with mass m, charge q and uniform B field.

B is going into the page, and particle is moving to the right enter image description here

Like this. The textbook says that the particle will go in a circular motion with a centripetal acceleration due to the force by magnetic field.

Also, I was taught that the formula for the force of magnetic field is F(vector) = q*V x B. However, the formula for this particular situation, the text book says it's F = qVB.

What happened to the cross product? I considered the angle formula for cross product ||A x B|| = ||A||*||B||*sin(theta). However, the force formula does not have magnitude signs over V nor B. So How did it get converted to qVB ?

  1. What does it mean by static B field, and how does it do 0 work on a free charged particle evne in a non uniform B field?
Qmechanic
  • 220,844
Hello
  • 71

1 Answers1

0

The magnetic force acting on a charge $q$ moving with a velocity $v$ through a uniform magnetic field $B$ is give by:

F = qv×B

It's magnitude is give by :

$F$ = $qvBsinθ$

where θ is the angle between the velocity of the charge and the direction of magnetic field.

Now, about your question:

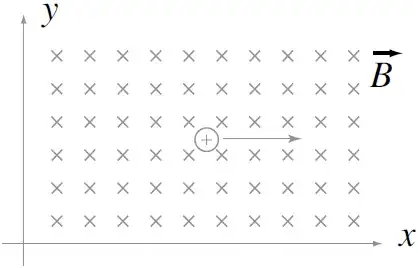
1) You have a magnetic field B pointing into the page. The particle is moving to the right through the magnetic field. So here, the velocity v is perpendicular to B. So the magnitude of force will be

$F = qvBsin 90 = qvB$

The direction of this force is given by the right hand palm rule. Suppose your four fingers (other than the thumb) point in the direction of the applied magnetic field. Let the thumb point in the direction of the velocity of the positive charge. Then the force will direct outwards from your palm. Applying this rule, the magnetic force is to the upward (y) direction. This force deflects the charge. A force creates an acceleration. But here the acceleration produced is by changing the direction of the charge. Magnetic force cannot speed up or slow down a charge. the reason why will be explained in the answer to your second question. So the particle traces a circular trajectory in the xy plane, whose centripetal acceleration is provided by the magnetic force on the charge.

The magnetic force, as you can see from the figure, will be maximum if the charge moves in a direction perpendicular to the applied field. There will be no magnetic force on the charge if the charge is not moving ($v=0$) or moves parallel or anti parallel to the magnetic field.

2) A static magnetic field means the magnetic field is not changing with time. A magnetic force do no work, whether static or not. We can derive it. Suppose we have a charge q moving with a uniform velocity v through a magnetic field B. Let the charge travels a distance dl in dt time, so that

v = dl/dt or

dl = vdt

The magnetic force acting on the charge is

F = qv×B

Now the work done by this magnetic force to move the charge a distance dl is given by

$dW$ = F.dl = (qv×B.dl) = q(v×B).dl

Now, substituting for dl,

$dW$ = q(v×B).vdt

Here you should note that the direction of (v×B) acts in a direction perpendicular to the plane containing both v and B. So, the dot product of something acting in a direction perpendicular to v with v gives zero. This is because dot product of two vectors give you the component of a vector in the direction of other. Here we have two perpendicular components and so their dot product is zero.

So we get

$dW = 0$

Hence

$W = 0$

This means the work done by a magnetic field to displace a charge from one point to another is zero. But it could accelerate a charge. A change in acceleration accounts by change in velocity w.r.t time. Here the change in velocity is not due to change in the magnitude of velocity, but due to change in direction of velocity. This causes acceleration. As far as the applied field is uniform, the magnetic force will be uniform and the charge maintains a circular motion with uniform acceleration at a constant radius, with the necessary centripetal acceleration provided by the magnetic force. But the magnetic force cannot speed up or slow down a charge.

If the applied field is time-varying then the force will also vary and the particle change the radius of circular trajectory, which result in a helical like motion. This means there is a net displacement along the direction of applied field. However in that case also, the work done by a magnetic field is zero. The work done to speed up the particle is done by the induced electric field generated by the changing magnetic field as per Faraday's law. The electric field can do work.

Remember that in deriving the work done by a magnetic force is zero, we haven't used any constraint that the field is uniform, about the particle's velocity etc. This means the rule is valid in all cases.

UKH
  • 5,021