Confusion about the shock growth

Question

I am studying Hamilton's & Blackstock's Nonlinear Acoustics. One of the essential phenomena associated with a finite-amplitude (unidimensional, planar) sound propagation is building the shock due to the super- and subsonic propagation speeds at different phases. The sound propagation speed is:

$$ c(t)=c_0+\beta u(t) $$

where $c_0$, $\beta$, $u$ denote adiabatic sound speed, coefficient of nonlinearity and acoustic velocity respectively.

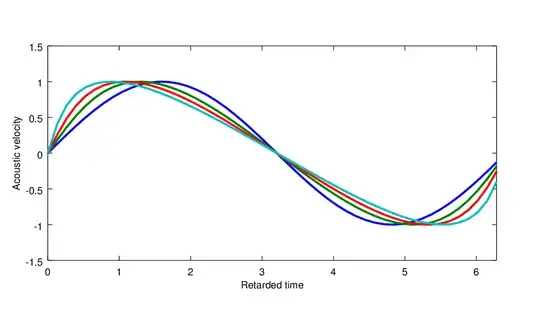
Distorted waveform is usually depicted in retarded time at various positions (from undisturbed blue to teal):

I don't fully comprehend why the positive (and therefore quicker) parts appear to be retarding and eventually making a N-like sawtooth wave? I would guess the mirror image of this process. Most probably I have a misconception in comprehending the retarded time.

Answer 1

I don't fully comprehend why the positive (and therefore quicker) parts appear to be retarding and eventually making a N-like sawtooth wave?

I wrote a more detailed answer at https://physics.stackexchange.com/a/139436/59023, but the basic idea is that the larger amplitude parts of the wave have a higher phase velocity than the lower amplitude parts. Thus, the larger amplitude parts outrun the lower amplitude parts, which is called nonlinear wave steepening.

In an unmagnetized fluid, the mathematical term that is important (often called the nonlinear term) is $\mathbf{V} \cdot \nabla \mathbf{V}$ and its magnitude relative to any loss terms (e.g., wave dispersion, viscosity, etc.)

Most probably I have a misconception in comprehending the retarded time.

In this example, the retarded time is just a time lag used to re-center each image so that the middle of the wave period stays in the middle of the plotting window. It's similar in concept to superposed epoch studies. You can use this to show a time evolution of something all in one plot, or your could produce a movie showing the evolution in time as well.