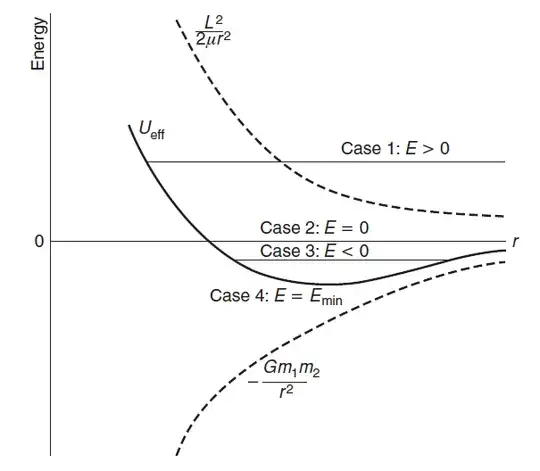
Consider the following energy diagram for the motion of a planet about a star.
The centrifugal potential curve can be represented once I fixed the angular momentum $\vec{L}$ of the planet. To fix the angular momentum vector of a planet in a orbit I have to fix not only its velocity vector $\vec{v}$ but I must fix this vector at a particular distance $\vec{r}$ from the point $O$. Is this correct?
Now suppose to fix the mechanical energy of the planet $E$ instead (i.e. the horizontal line cannot change). Suppose that I can change the angular momentum of the planet, for istance I can move approximately up or down the centrifugal potential curve. For fixed $E>0$ values, if $L$ grows, the minimum distance approached by the planet from the star increases too. But consider the ellipse situation, i.e. $E<0$. If I move up the centrifugal potential curve the perihelion gets further (and that seems right) but the aphelion gets closer to the star. I don’t see the reason of this last fact, if the planet rotates faster ($L$ increases) shouldn’t it get further both in the min and max distance in its orbit?
Is there something I am missing here?