Logan R. Kearsley asked: "what's the correct way to calculate these quantities (proper orbital period and proper orbital velocity) in terms of r, M, and a?"
The circular velocities relative to a ZAMO in the equatorial plane and can be found by setting the coordinate acceleration (assuming we use pseudospherical Boyer Lindquist or Doran Raindrop coordinates) and all velocities except the tangential velocity to zero and solving for the remaining velocity component, the pro- and retrograde solutions in natural units of $\rm{G=M=c=1}$ are:
$$\rm v_{\pm}=\frac{a^2 \mp 2 a \ \sqrt{r}+r^2}{\sqrt{a^2+(r-2) \ r} \ \ \left(a \pm r^{3/2}\right)}$$
The local velocity of a ZAMO relative to the fixed background is
$${\rm v_z} = \sqrt{g_{\rm t \phi} \ g^{\rm t \phi}} = \sqrt{1 - g_{\rm t t} \ g^{\rm t t}} = \rm \frac{2 a \ \sqrt{\frac{a^2 \ (r+2)}{r}+r^2} \ \ \sqrt{\frac{4}{a^2+(r-2) \ r}+\frac{2}{r}+1}}{a^2 \ (r+2)+r^3}$$
($\rm v_z=1$ at $\rm r=2$ where the ergosphere has its equatorial edge), while the equatorial circumference in the frame of the ZAMO is
$${\rm U}_{\phi}=2 \pi \ \sqrt{|g_{\phi \phi}|}=\rm \frac{2 \pi}{r} \ \sqrt{\left(a^2+r^2\right)^2-a^2 \left[a^2+(r-2) \ r\right]}$$
so the orbital period in terms of the proper time of the orbiter is
$$\rm \tau = \frac{U_{\phi} \ \sqrt{1-v_{\pm}^2}}{v_z + v_{\pm}}$$
Example: a prograde orbit at $\rm r=3$ with $\rm a=1$ has a local velocity of $\rm v_{+}=0.527416$, a ZAMO velocity of $\rm v_z=1/3$ and a circumference of ${\rm U}_{\phi}=20.5208$, so $\tau=20.2552$:
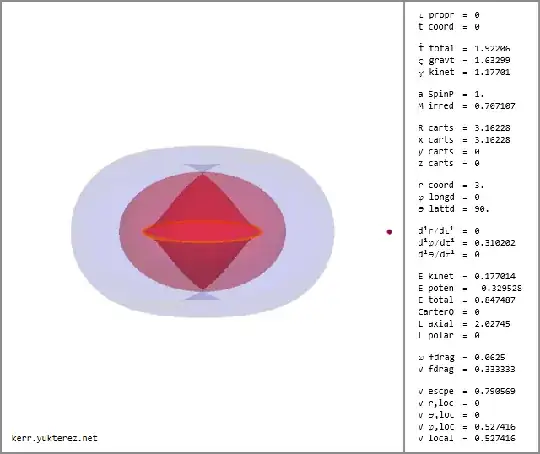
A retrograde orbit would not be possible at this $\rm r=3$, since for $\rm v_{-}$ to be larger than $-1$ (smaller than the speed of light) we need $\rm r>4$ in this example with $\rm a=1$ (with $\rm a=0$ we would get $\rm v_{+}=1$ and $\rm v_{-}=-1$ at $\rm r=3$, where a Schwarzschild black hole has its photon sphere).
An alternative way is to set $\rm \ddot{r}=\dot{r}=\dot{\theta}=0$ and solve for $\dot{\phi}$ (overdot is differentiation by proper time $\tau$), then you get $\dot{\phi}_{+}=0.310202$ for the prograde solution, if you divide $2 \pi$ by that you get the same result for the time:
$$\dot{\phi}_{\pm} = \rm \frac{\pm \sqrt{a^2 \ (r+2) \ r^5+r^8} \pm a^2 \left[\sqrt{a^2 \ (r+2) \ r+r^4}+2 \sqrt{\frac{a^2 \ (r+2)}{r}+r^2}\right]}{\sqrt[4]{r} \ \surd \left[ \pm 2 a+(r-3) \surd r \right] \ \left[ a^2 \ (r+2)+r^3\right]^{3/2}}$$
The proper time in the ZAMO's frame is longer by a gammafactor of $\rm 1/\sqrt{1-v_{\pm}^2}$, but note that this is not the time for the orbiter to meet the ZAMO twice, but the time for the orbit to make a revolution of $360°$ where he sees the same stars as at the beginning of his orbit (the ZAMO himself has moved on in the meantime as you can see on the smaller dot in the animation).
If you are not looking for the time it takes for one full revolution, but the time it takes the orbiter to catch up with the ZAMO he overtook at the start position the proper time in the orbiter's frame is
$$\rm \tau = \frac{U_{\phi} \ \sqrt{1-v_{\pm}^2}}{v_{\pm}}$$
(which is $\tau=33.0567$ in this case), and without the gamma factor in the ZAMO's frame (that is $\rm {}_T=38.9082$). At this position they don't see the same stars they saw at their initial position.
In the frame of the coordinate bookkeeper at infinity the ZAMO's time is multiplied with
$$\sqrt{g^{\rm tt}}=\rm \sqrt{\frac{4}{a^2+(r-2) \ r}+\frac{2}{r}+1}$$
so the time for one $360°$ revolution in this frame and with said parameters is $\rm t=38.9316$ and $\rm t=63.5368$ until the orbiter meets the ZAMO for a second time.
The orbit velocity $\hat{\rm v}_{\pm}$ relative to the fixed stars or a locally stationary observer not corotating with the black hole (who can only exist outside the ergosphere) is calculated with the relativistic velocity addition formula of the ZAMO's velocity and the orbit velocity relative to the ZAMO:
$$\hat{\rm v}_{\pm} = \rm \frac{v_z + v_{\pm}}{1 + v_z \ v_{\pm}}$$
which in this case is $\hat{\rm v}_{+} = 0.732051$ for the prograde solution.
All $\rm v$ are in units of $\rm c$, the angular velocity $\dot{\phi}$ in $\rm c^3/G/M$, the $\rm r$ in $\rm G M/c^2$ and times in $\rm G M/c^3$. The equations here assume $\theta=\pi/2=90°$ (the equatorial plane), if we also allow polar velocity components the equations become much longer.
For more information see Bardeen at al (1972), page 14+. In case I made a typo in the Latex or if you get confused by the $\pm$ and $\mp$ in the solutions click here for a screenshot of the working worksheet.
