Rapid acceleration does what to inertial frame clocks?

Question

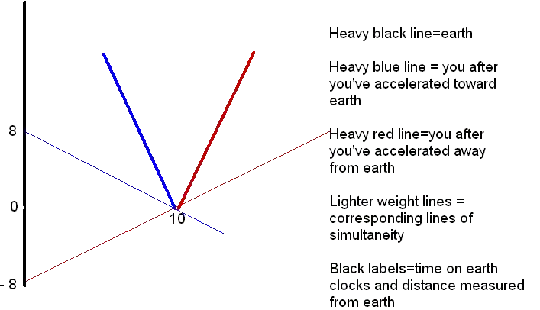
I'm 10 light years from Earth and see Earth's clock/calendar reading 2000, including light travel time. In other words, I assume it's 2010 on Earth, but what I actually see is the year 2000 due to light travel time.

I now accelerate towards Earth to 0.8c in one second. What does Earth's calendar read to me now, including light travel time? The two answers I appear to be getting from my related question:

• You still see Earth's calendar at the year 2000, plus maybe a few seconds.

• You see Earth's calendar at 2004 (for example): it has jumped ahead several years during your acceleration.

I'm getting a variety of interesting answers to Rapid (ac/de)celeration in relativity does what to inertial clocks? but I don't think they're all consistent, which is perhaps my fault for phrasing the question ambiguously. I'm hoping this question is less ambiguous.

EDIT: This question is not a duplicate of my Rapid (ac/de)celeration in relativity does what to inertial clocks? because that other question involves acceleration, constant speed travel, deceleration, and ignores light travel time.

I believe this question is much simpler, although I agree the two are related.

The Fargo Fallacy

This section is in response to @WillO's and @hypnosifl's "driving to Fargo" analogy.

@WillO states

I am driving north toward Fargo. I say "Fargo is straight ahead, and always has been". Now I make a left and say "Fargo is to my right, and always has been".

[...]

Do you really not understand that this is shorthand for "Fargo is in the direction i now call right and always has been?" Or that my previous reckoning of Fargo as straight ahead has now become completely irrelevant? Or that if I continue to rely onthat [sic] reckoning, I'm going to get lost?

The statement "Fargo is to my right, and always has been is fundamentally inaccurate and can not be justified as shorthand.

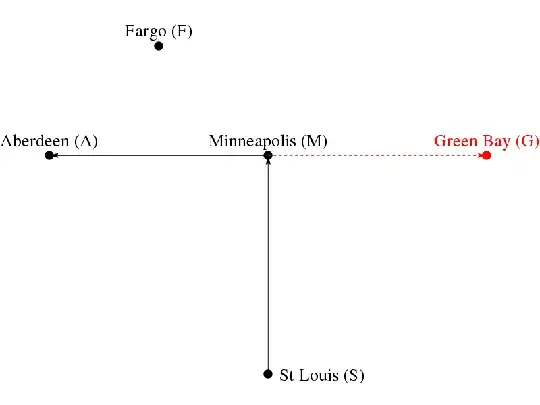
Suppose I'm in Aberdeen and want to know where I was two hours ago (each arrow represents one hour). Using @WillO's logic, I must assume that Fargo was always to my right, and I was thus in Green Bay two hours ago.

In reality, my previous reckoning of Fargo is relevant. Here are some legitimate statements I could make:

• For one hour, I was traveling from St Louis to Minneapolis, and Fargo was (pretty much) straight ahead.

• For one hour, I was traveling from Minneapolis to Aberdeen, and Fargo was (pretty much) to my right.

• If someone else had been traveling the Minneapolis-Aberdeen path an hour before I got there, arrived at Minneapolis at the same time I did, and was traveling at the same constant speed as I am traveling, they would have been in Green Bay when I was in St Louis.

• Another way to say it: one hour after starting out, I hopped on to a ghost train that is doomed to travel forward westward at constant speed. I hopped on the train at Minneapolis and it took me an hour to get to Aberdeen. I can thus conclude the train was in Green Bay one hour ago, when I was in St Louis.

Converting any of these statements to Fargo is to my right, and always has been isn't "shorthand", it's simply false.

Fundamentally, the Fargo Fallacy confuses the history of an observer and the history of a reference frame. The "ghost train" in my example above is a reference frame: it always travels in the same direction at the same speed. However, the observer (me) wasn't on the train before it arrived at Minneapolis. In fact, it's possible that there was no one at all on the train on its journey from Green Bay to Minneapolis.

Once we understand this difference, and note that reference frames can exist without anyone in them, we can solve the problem. Ideally, we could solve this problem without using unpopulated reference frames (no ghost trains) at all. I'm checking to see if this may be possible, more details if that pans out. As @hypnosifl notes, bringing "north" into it breaks the analogy because "north" has some objective definition that doesn't depend on our choice of coordinate system. If we did have such a "north" in relativity, everything would be a lot easier, because we wouldn't have to rely on relative directions. Unforunately, the entire concept of special relativity is that all frames are relative.

The Fargo Fallacy also appears in Question/Doubt about Time Dilation Symmetry in Special Relativity: if two objects are 8 light years apart when at rest and approach each other, there is no frame of reference in which they will ever be more than 8 light years apart. However, one of the answers states:

when the light signal was sent, I was not just 4.8 light years away; I was 4.8 plus another (10.67 x .8) light years away --- a total of about 13.33 light years.

Once again, the confusion is between observers ("I") and reference frames. It was the reference frame that was 13.33 light years away, not the observer (who was never more than 8 light years away).

The 10/6 Conundrum

Consider this event: a beam of light leaves Earth in the year 2000.

Before I accelerate, this event occurs 10 light years away from me 10 years ago (since I am just now seeing this light beam). In other words, my coordinates for this event are $\{10,-10\}$ (note: I've re-oriented the x axis to face Earth, since that's the direction I will be traveling, but the conundrum occurs regardless of x axis orientation).

After I accelerate, I'm seeing the same light beam (roughly speaking), but the Earth is now only 6 light years away. I thus conclude the light beam left Earth 6 years ago (in my reference frame). Thus, my coordinates for this event are $\{6,-6\}$.

I suspect there's something wrong with my setup above, but can't figure out what it is.

Why am I suspicious? If the above is correct, the Lorentz transform for $0.8 c$ should convert between the two coordinate systems, but it doesn't.

Instead, it converts $\{10,-10\}$ to $\{30.,-30.\}$ (this is the same answer as @WillO gets), which says that, in the new, accelerated, frame, the light beam left Earth 30 light years away from my frame 30 years ago. Of course, I wasn't in this frame at the time: I only entered the frame in the year 2010 at t=0.

Oddly enough, it turns out the Lorentz transform for $-\frac{8 c}{17}$ does convert $\{10,-10\}$ to $\{6,-6\}$, but I have no idea how that velocity (a little less than $0.5 c$ and going in the opposite "wrong" direction [ie, away from Earth]) enters the picture.

Changing our definition of t=0 doesn't appear to help either. The $0.8 c$ Lorentz transform of $\{10,u-10\}$ is $\left\{30-\frac{4 u}{3},\frac{5 u}{3}-30\right\}$. There is no value for $u$ which yields $\{6,-6\}$.

Setting $u=18$ yields $\{6,0\}$ (which is interesting) giving us the correct distance, and setting $u=\frac{72}{5}$ yields $\left\{\frac{54}{5},-6\right\}$ giving us the time, but neither of these yields $\{6,-6\}$

Again, I feel I've done something wrong in setting up the above.

On the one hand, I have two reference frames, and the Lorentz transform should be able to convert between them, since it accounts for time dilation, Lorentz contraction and simultaneity.

On the other hand, well, it doesn't seem to actually do that.

Answer 1

If you accelerate toward the earth, you say that the earth clocks have jumped forward 8 years. If you accelerate away from the earth, you say that earth clocks have jumped backward 8 years (give or take a small correction for the fact that you spread your acceleration over a second rather than accelerating instantly).

What you see on earth's clocks is of course essentially unchanged. (It would be completely unchanged if your acceleration were instantaneous.) This is because the light rays arriving at your ship are not going to divert their courses just because you happened to accelerate.

(Picture assumes instant acceleration; second-long acceleration introduces small corrections.)

Answer 2

Either way your time would slow down compared to Earths time while you where accelerating but I think the final difference between the two would depend on the direction you had traveled. Moving toward the Earth would be slightly different than moving away from Earth.

Answer 3

This additional detail is in response to the comment thread on my earlier answer. It provides every step of the calculations, which are perfectly standard and the sort of thing you will find in any reputable textbook. They are also exactly equivalent to what's going on in the spacetime diagrams you're curiouosly reluctant to study.

Start by labeling some events.

Event A: The spaceship suddenly accelerates to earth, with its clock saying 2010.

Event B: A clock on earth says 2000

Event C: A clock on earth says 2010.

Event D: A clock on earth says 2018

Frame I is the ship's frame an instant before the acceleration. In this frame, event $A$ is the origin, so event $A$ takes place at location $x=0$, time $t=0$.

In Frame I, Earth is 10 light years to the left of the spaceship, so events B,C and D take place at location x=-10. They occur at times $t=-10$, $t=0$, and $t=8$.

Now let's find the locations and times of these events in Frame II. We'll call those locations and times $x'$ and $t'$. We get these from formulas $x'=(x+tv)/\sqrt{1-v^2}$ and $t'=(t+xv)/\sqrt{1-v^2}$.

For event $A$, $x=0$ and $t=0$ (and $v=.8)$ so the Lorentz transform gives $x'=0$ and $t'=0$. That is, the switch from Frame I to Frame II does not change the coordinates of this event.

For event $B$, $x=-10$ and $t=-10$, so the Lorentz transform gives $x'=-30$, $t'=-30$. That is, in Frame II, this event took place 30 light years away and 30 years ago. Therefore its light is just arriving at the origin.

For event $C$, $x=-10$ and $t=0$, so the Lorentz transform gives $x'=-16.67$ and $t'=-13.33$, so this event took place $16.67 light years away and 13.33 years ago.

For event $D$, $x=-10$ and $t=8$, so the Lorentz transform gives $x'=-6$ and $t'=0$. That is, this event is taking place 6 light years away and is happening right now.

Notice that both frames have to describe the same reality. So here's a reality check: In Frame I, event B is 10 light years away and 10 years ago, so its light is just arriving at the origin. In Frame II, event B is 30 light years away and 30 years ago, so its light is just arriving at the origin. Sure enough, the frames agree --- as they must, because that light either does or does not arrive at the origin.

If the two frames were to disagree on what's actually happening at the origin, you'd know there was a mistake in the arithmetic. Because they agree, you can be pretty confident there's no mistake.

Answer 4

I'm 10 light years from Earth and see Earth's clock/calendar reading 2000, including light travel time.

In other words, you see, literally physically see, the clock reading that time.

In other words, I assume it's 2010 on Earth,

This is the root of all the confusion. You shouldn't assume that; it's meaningless. Coordinate systems are meaningless. I don't know why so many people (including teachers) imagine that you have to use a coordinate system in which you're instantaneously at rest, and that people moving differently "disagree" with each other because they insist on using their self-centered coordinate system and saying that everyone else's is wrong. That's the exact opposite of the truth. The universe doesn't care about coordinates. If you have to use them (which you probably do because coordinate-free physics is more difficult than coordinate-free Euclidean geometry), then pick whatever makes the problem easiest, and don't switch between coordinate systems in the course of solving a single problem unless you really understand what you're doing, because it will most likely just lead to confusion and mistakes.

I now accelerate towards Earth to 0.8c in one second. What does Earth's calendar read to me now, including light travel time?

I'll assume that you accelerate uniformly, and it's one second of your proper time. Then with respect to coordinates in which you start accelerating from rest at $t=\tau=0$, and Earth is at rest far in the +x direction, and using natural units for the acceleration, your spacetime location as a function of your proper time is $(x(\tau),\ t(\tau)) = (\cosh(\tau), \ \sinh(\tau))$. Your velocity as a function of proper time is $x'(\tau)/t'(\tau) = \tanh(\tau)$ (those are derivatives, not primed coordinates). The reading on Earth's clock (up to an additive constant) as a function of your proper time is $x(\tau) + t(\tau) = e^\tau$. Plugging in 0.8 for your final speed, you get $\tau_f = \tanh^{-1}(0.8) = \ln 3$, and $\tau_i = 0$, so one second is $\ln 3$ in these units. The change in the reading of Earth's clock during your acceleration is $e^{\ln 3}-e^0 = 2$ exactly, or in SI units, $2/\ln 3 \approx 1.82$ seconds. (If I didn't screw up somewhere.)

I did this using coordinates because coordinates are often very convenient for solving physics problems. But it doesn't matter which coordinate system I used. I didn't choose coordinates in which you're instantaneously at rest throughout your acceleration, or in which anything is ever at x=0. I didn't even use standard units of distance or time. If I'd made any other choice, I would have gotten the same answer to any physically meaningful question, such as what you'll see on an actual clock with your actual physical eyes. I would not necessarily have gotten the same answer to meaningless questions such as what's allegedly going on "now" at some distant location according to some crazy person who insists that the coordinate time of their current favorite reference frame is the one true universal synchronous time.

The Fargo Fallacy

When you talk about the "Fargo Fallacy," I think you understand that you're just playing word games. Nothing about the nature of Fargo or your trip is at issue; it's all about what the word "right" means, and words can mean different things to different people. There is no experiment you can do to decide who's right about the meaning, because the universe doesn't care.

"Now" (except in combination with "here") is just like "right" in this regard. You'll never find its true meaning. It doesn't need to have one because it plays no role in any physical theory. Nothing in modern physics depends on a notion of distant simultaneity, and as far as we can tell, nothing in the real world does. I know I'm repeating myself but people so frequently get this so wrong that I feel like I have to beat it out of them.

The 10/6 Conundrum

[...]

Before I accelerate, this event occurs 10 light years away from me 10 years ago (since I am just now seeing this light beam). [...] After I accelerate, I'm seeing the same light beam (roughly speaking), but the Earth is now only 6 light years away.

No, it isn't. It may be 6 ly away in the coordinate system that you've just decided to switch to in the middle of solving your problem. Relativity doesn't require you to be so self-centered.

I thus conclude the light beam left Earth 6 years ago (in my reference frame). Thus, my coordinates for this event are {6,−6}.

I think you're simply overlooking that the Earth is not at rest with respect to these coordinates. When you plugged 0.8 into the length contraction formula, what you got is the intersection of the Earth's worldline (idealized as inertial in this problem) with the line $t' = 0$. That intersection is at $(x',t') = (6\,\mathrm{ly},0)$. Earth's worldline is the unique line through that point with the right slope, namely $x' = 6\,\mathrm{ly} - 0.8t'$. The intersections of that worldline with your light cone are the solutions of $\{x' = 6\,\mathrm{ly} - 0.8t',\; x'^2 = t'^2\}$, namely $(x',t') \in \{(30,-30),(10/3,10/3)\}\,\mathrm{ly}$.

Just think of it as Euclidean geometry, because it almost is, up to a minus sign in the Pythagorean formula. When using coordinates, you have to keep coordinate tuples together. It doesn't make sense to talk about y alone or t alone. (Except, I suppose, when there's a line with the equation y or t = constant. But such lines generally don't occur in nature, because the universe doesn't understand or respect any inertial coordinate system's idea of distant simultaneity.)

What the length contraction formula answers is the following question: you have a straight strip of uniform width in the Euclidean plane. When measuring its width along a line perpendicular to it, you get $w$ (say). If you measure along a line inclined at 45° to the perpendicular, you get a larger value, $w\sqrt2$. In general, along a line inclined at angle $\theta$, you get a width of $w\sec\theta$. The Minkowskian equivalent is $w\,\mathrm{sech}\,\alpha$, where $\alpha$ is the rapidity. It may look more familiar if you use the slope: for a slope $v$, the Euclidean formula is $w\sqrt{1+v^2}$ and the Minkowskian formula is $w\sqrt{1-v^2}$. The sign difference comes directly from the sign difference in the metric.

Why would you care about the width of a strip measured along a line that doesn't respect its intrinsic symmetry? You probably wouldn't, unless you're taking an undergraduate physics test set by a professor who thinks that this particular sort of measurement is extremely important for some reason.

Answer 5

Rapid acceleration does what to inertial frame clocks?

Nothing much. Like I said in response to your previous question.

I'm 10 light years from Earth and see Earth's clock/calendar reading 2000, including light travel time. In other words, I assume it's 2010 on Earth, but what I actually see is the year 2000 due to light travel time.

OK, that's nice and simple.

I now accelerate towards Earth to 0.8c in one second. What does Earth's calendar read to me now, including light travel time?

Pretty much the same. Your second is time-dilated compared to the Earth second, and the difference is a couple of tenths of a second. Not 14,000 seconds. The Andromeda Paradox is another one to beware of. You know full well that the time now on Earth doesn't change back and forth by 8 years when you accelerate and decelerate. You have a spaceship, not a time machine. And you felt the acceleration. You know that the Earth hasn't always been moving towards you.

The two answers I appear to be getting from my related question: 1) You still see Earth's calendar at the year 2000, plus maybe a few seconds. 2) You see Earth's calendar at 2004 (for example): it has jumped ahead several years during your acceleration.

The former is correct.

I'm getting a variety of interesting answers to Rapid (ac/de)celeration in relativity does what to inertial clocks? but I don't think they're all consistent, which is perhaps my fault for phrasing the question ambiguously. I'm hoping this question is less ambiguous.

I don't think your previous question was ambiguous.

This question is not a duplicate of my Rapid (ac/de)celeration in relativity does what to inertial clocks? because that other question involves acceleration, constant speed travel, deceleration, and ignores light travel time.

Fair enough. And like John Rennie said, at 0.8c it takes you 12.5 years to travel the 10 light years to Earth, during which time you see the Earth's calendar advance by 22.5 years because the light-travel-time is reducing as you approach.

I believe this question is much simpler, although I agree the two are related.

IMHO it's all very simple. Simpler than you might think.