The question state that 2 large parallel plates are a distance $d$ apart and the field at $d/2$ is $E$ if the distance between the plates are reduced to $\frac{d}{2}$ what is the field strength halfway between the 2 plates?
I have found 2 possible ways 2 solve this online
$E=\frac{V}{d}$ and another formula $E=\frac{\sigma}{2\epsilon_0}$ in the last equation the distance between the plates does not factor.
Why are there 2 ways? this seems to be contradictory and I am not sure what to do.
The exact formula to calculate the electric field at a distance $z$ from the centre of a disk of radius $R$ is given at
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html
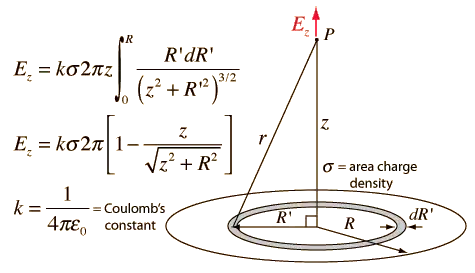
As you can see for $R\gg z$ the magnitude of electric field is constant and given by $E=\frac{\sigma }{2\varepsilon_{0}}$.
The $V=Ed$ formula can be applied to the case where two parallel plates kept at voltage $V$ (external) and separated by distance $d$. See the animation below from
http://www.regentsprep.org/Regents/physics/phys03/aparplate/
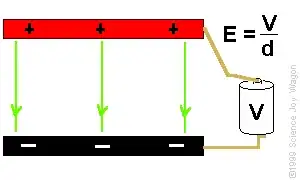
As you can see if the potential is constant as the distance gets smaller the electric field increases. If you want to apply the $E=\frac{\sigma }{2\varepsilon_{0}}$ formula here you need to calculate a new $\sigma$ for each $d$ because in this case $\sigma$ is not constant, it increases as the plates come closer as illustrated in the animation by more $+$ and $-$ charges on the plates.
Edit: Answers to the questions in the comments.
Question: What is $\sigma$ and why it increases as the two plates come together under a constant external potential $V$?
Answer: $\sigma$ is a measure of charge density. It can be calculated as total charge divided by total area. $\sigma$ increases as the plates come closer because the charges on each plate can attract more of the opposite charge to the other plate.
Question: How would one calculate the new electric field if the distance between the plates is reduced but there is no external voltage, that is the plates has constant $\sigma$?
Answer: There are two ways. If the $R\gg z$ case is valid then irrespective of the distance between the plates the electric field is constant and given by $E=\frac{\sigma }{\varepsilon_{0}}$.
If $R\gg z$ is not valid then one needs to use
$$E_{z}=\frac{\sigma}{2\varepsilon_{0}}\left ( 1-\frac{z}{\sqrt{z^{2}+R^{2}}} \right )$$
to calculate the electric field.
You are confusing the relationship of $V$ to $E$ with the definition of $V$.
The E-field at a point in space depends on the distribution of charge around that point. That's the primary determining factor. The potential difference between the plates (or between two points in space) is defined based on what the E-field is : $$V_{ab}=\int\limits_{r_a}^{r_b}\vec{E}(\vec{r})\cdot d\vec{r}$$
Now, you have to apply this to your specific geometry (small gap between two parallel plates). Remember that the E-field depends on where the charges are. How does the $E$-field vary close to a sheet of uniformly-distributed charge?
The $V$ (potential difference) depends on how the $E$ varies between the two points and how far apart the charges are.
