Let's see how the units work out if we convert a linear spring (where we know everything) to a torsion spring, by attaching our linear spring to a stiff rod some distance $R$ from a pivot:
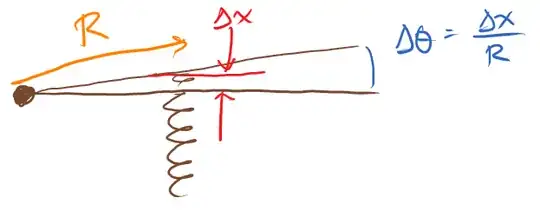
The (linear) force due to the spring is $\vec F = -k\Delta \vec x$, for spring constant $k$ having units of newtons per meter. The torque is
$$
\tau = RF = -R \cdot k (R \Delta\theta) \equiv -\kappa \Delta\theta
$$
So apparently the torsion spring constant $\kappa = kR^2$ has units of newton-meters, which is equivalent to newton-meters per radian, because the radian is a dimensionless ratio. If you mistrust the apparatus of calculus and would like to do a lot more work you could use the appropriate trig function $\sin\Delta\theta = \Delta x /R$; in that case only follow my argument in the small-angle approximation $\lim_{|x|\ll1} \sin x = x$.
The energy stored in the linear spring is
\begin{align}
U = -\int_0^{\Delta x} \vec F \cdot d\vec x
= \frac12 k(\Delta x)^2 = \frac12 k(R\Delta\theta)^2 = \frac12 \kappa (\Delta\theta)^2
\end{align}
which is exactly the same thing you get if you integrate the torque
$$
U = -\int_0^{\Delta\theta} \vec\tau \cdot d\vec\theta = \frac12 \kappa (\Delta\theta)^2
$$
As another answer says much more succinctly: it all works because the radian, a ratio between two lengths, is dimensionless.
lemon asks in a comment elsewhere how you would convert $\kappa$ in each case if you were tied to a log in a sawmill and commanded either to use degrees or die a hideous bloody death. (My paraphrase; I would probably choose death, myself.) In that case you might grudgingly admit that the relevant constant in the torque equation has units of foot-pounds per degree, while in the energy equation you have picked up another angular factor so that the unit is b.t.u. per degree squared. I don't think there's anything profound about the coincidence that torque has units of energy; I do think there's something profound about the fact that we have invented the SI units to make these pointless problems go away.
