-1

Last time I brought this up, the best answer featured an image that looked something like this:

enter image description here

The argument here is that as the distance increases between the eye and the object, the angle gets smaller. It's not even a physical phenomenon: it's a geometrical phenomenon.

Fine. Let's look at this from a different angle, no pun intended.

The diameter of the human eye lens is roughly 10 mm. According to the above logic, an object whose size is smaller than that (say a raindrop) should NEVER decrease in size while the distance increases, and should remain visible no matter how far away it is (Pluto's orbit and beyond):

enter image description here

What am I missing?

Community
  • 1
Ricky
  • 641

2 Answers2

6

You are missing at least two things:

  • The eye is a focusing optical system. When the eye is focused for non-infinite distance those parallel rays reconstruct to different parts of the retina; that is to say that the image having finite size does not depend on the object being larger than the focusing element.

  • The light leaving objects is diverging resulting in the amount of light reaching the eye to decrease with increasing distance. And this, too, is not affected by the relative size of the object and the focusing element.

If I can be allowed to offer a word of advice, you've reached the point where you need to stop asking "explain to me in simple words" and actually dig in and understand the physics. The explanation is very simple, but you have to have the right framework and vocabulary in which to understand it. The framework you want for this question is ray optics.

dmckee --- ex-moderator kitten
  • 87,238
2

"According to the above logic, an object whose size is smaller than that (say a raindrop) should NEVER decrease in size while the distance increases." This is false!

The logic says that a good simple model of a camera is a pinhole camera/camera obscura. This is nice, because the aperture can be idealized as a point with no spatial extent. The plus side of a camera obscura is that you aren't really going to have depth of field blurring. The downside is that the image is very dim. You imply in your question: you understand why things appear in perspective for a pinhole camera.

Unfortunately, nature has said, (for the most part) nope, not good enough, we need a better eye to survive in the wild. We use a lens, retina, and a larger aperture. That's where your confusion comes in. What the heck goes on with a larger aperture? Without a lens, you'd just have a mash of colors hitting your retina. Without a lens, a point on any object would have ray trajectories to any visible point on your retina, and light from every object would distribute itself over the whole retina, and you'd just see a blur.

So your insistence on a finite size aperture means that you now need a lens... well great, how could something possibly focus light? Paraphrasing my answer on another post:

You can't just magically change the direction of a ray of light, you have to do it by mere mortal means, in the form of a slab of glass. Even simple lenses act in a way that's rather complicated.

If you're really insistent that you aren't satisfied with the pinhole camera explanation, you need ray optics. You need Snell's law, which tells you how glass works. You need the paraxial approximation, which gives you nice formulas for what lenses do. And you'll have to start worrying about depth of field and other things. You'll have to focus your camera differently depending on the distance to the raindrop you're worried about. And you'll find that all the details aren't that important!!!

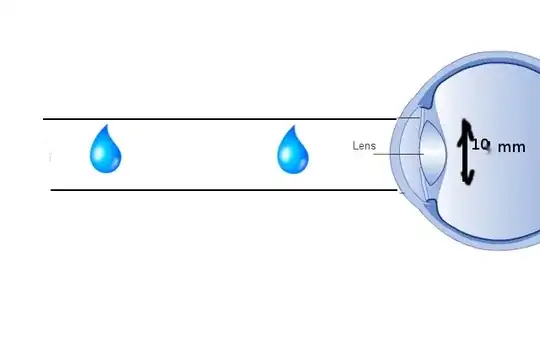
Try to work out the details with a lens focused at infinity, which takes in a tube of light rays from any direction and turns it into a point on your photosensitive surface. (ex. this page/image, where parallel rays of light are focused onto the same point). Giving it away: the specification "direction" $\mapsto$ "point on your photograph" means you're almost working with a pinhole camera again.

Community
  • 1