For my project, I need to create a lock gate which will be used for the Panama Canal. One of the many thing my teacher said, was that for the design of the lock gate, the gate should not fail when it gets bumped by a large ship (like a cruise ship).
All the information that we need to calculate, like the mass of a common cruise ship can be found on the internet or other places. We came to the conclusion that the mass of a cruise ship, in the worst case scenario, is equal to $65.000.000 \text{ kg} + 158.200.000\text{ kg} = 223.200.000\text{ kg}$.
The $65.000.000$ is the mass of a common cruise ship and the $158.200.000$ is the maximum mass a cruise ship can hold. The average speed of a cruise ship is equal to about $7 \text{ m/s}$.
We can now calculate the kinetic energy, which is:
$$E_k = \frac12mv^2$$
$$E_k = \frac12\cdot223.200.000\cdot7^2$$
$$E_k =5.468.400.000\text{ J}$$
But after this, I got stuck. A tip from my teacher was that we also need to use the formula $W = F\cdot s$, whereas $s$ is the indentation of the lock gate. How do I know that the lock gate will not fail? I wanted to try something like this:
$$\frac12mv^2 = F \cdot s$$
But I'm not sure if this is right. What is the right approach to know if a lock gate will fail or not against a bump of a cruise ship?
Edit
Here is the information about the lock gate:
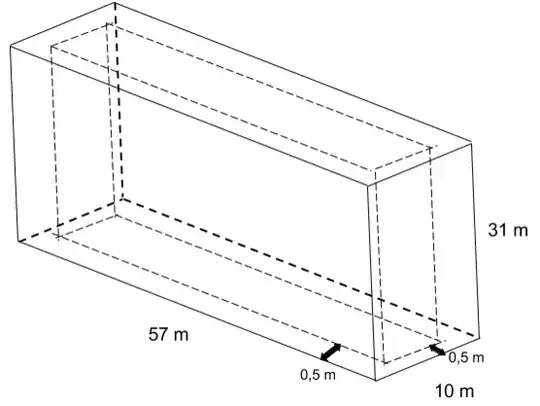
The lock gate itself is 31 m x 10 m x 57 m and is hollow in the inside. This leaves a 30 m x 9 m x 56 m gap:
The thickness of the edge is 0,5 m everywhere. The outer case is made of steel and has crossed steel beams.