What are the conditions for a heap of identical hard spheres to be in a static equilibrium?

Question

It is common to see a heap of conical shape formed by a large number of similar size hard spherical objects, for example, a heap of pebbles, sand etc. Suppose we want to model this system as a collection of identical hard balls, with dry friction between the balls described by coefficient $\mu_1$ and the friction between the balls and the floor described by coefficient $\mu_2$. Based on a "toy" problem with three cylinders forming a pyramid one can conjecture that there is some threshold condition for $\mu_1$ and $\mu_2$ that guarantees equilibrium for a heap. What are the conditions for a heap of identical hard spheres to be in a static equilibrium?

Answer 1

I don't have a full answer (which would probably require some computer simulations) but one can rather easily analyze a case of a regular pyramid in hexagonal close packing, assuming strong friction on the floor (non-slip condition). This would be something like a bunch of marbles on a rubber mat.

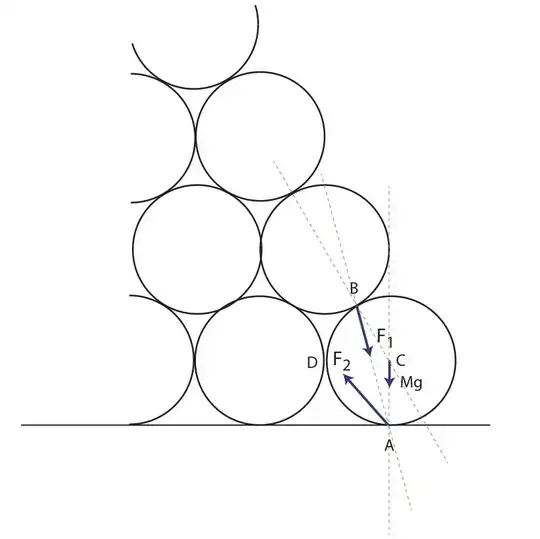
First look at it in 2D, so we have an arrangement like in the Figure. Consider the forces on the lower right cylinder. At the threshold of stability there is no force from the second right cylinder in the bottom row, and the lower right cylinder is at the threshold of slippage at point B (no slippage at point A by the assumption). The force $F_1$ from the top log applied at point B is directed towards point A so that there is no net torque on the lower right cylinder. Therefore we immediately find from the geometry the condition $\mu_1 \geq \tan(15^{\circ})$, otherwise the lower right cylinder would start rolling to the right.

Now, back to 3D; if there is a regular pyramid of identical spheres in the HCP packing then an outermost sphere in the bottom layer would have a single sphere in the layer above pushing on it. Then situation is analogous to the 2D case except instead of 60$^{\circ}$ for the angle DCB we would use $\arccos(\sqrt{2/3})$ (from the regular tetrahedron geometry) which is about 35$^{\circ}$. So in 3D the critical value of $\mu_1$ becomes $\tan(({90^{\circ}-\arccos(\sqrt{2/3})})/2) \approx \tan(26^{\circ})$. For a general packing this condition will probably still be necessary (but not sufficient) for the equilibrium to exist (if we exclude unstable arrangements such as the cubic lattice).

Answer 2

This is a semi-solved problem in civil engineering, where the angle made by a pile of small objects is called the angle of repose, which depends on the density, size distribution, and sharpness or irregularity of the objects in the pile. If the objects in the pile are randomly stacked, small compared to the size of the pile, and the coefficient of static friction between them is known, then an approximate solution for the angle of repose is

angle of repose = arctan(coefficient of static friction)