Is it possible to gravitationally redshift light so much that it reverses direction?

Question

I know that redshifting does not mean that light is actually going slower but rather just reducing the energy. Is there a point that the energy is actually reduced to zero and then continues to "negative/reverse" energy making the light go backwards?

Answer 1

Let's ignore gravity for a moment and think about the red shift that arises from relative motion. Suppose I shine a beam of green light at you while you are moving away from me at some velocity $v$. Because you're moving away from me you see the light as red shifted, and the faster you are moving away from me the bigger will be the red shift. As your speed relative to me approaches $c$ the red shift approaches infinity i.e. the light red shifts away to nothing.

To red shift the light any further you would have to increase your speed even more i.e. relative to me you would have to be moving faster than light. Of course this isn't possible, but leaving that aside it would mean that the light can never catch up to you - in effect you have managed to reverse its direction.

This can't happen in special relativity because you can never achieve a speed relative to me of faster than light. However it can happen in general relativity - well, sort of, depending on how you define velocity.

How you define velocities in a curved spacetime depends on what coordinate system you choose to work with. If we consider the gravitational field due to a black hole then with coordinates we normally use (the Schwarzschild coordinates) the velocity of light behaves rather strangely as we approach the event horizon because the Schwarzschild coordinates are singular there.

However we can choose different coordinates that do not have a singularity at the event horizon, and one of the simplest choices are the Gullstrand-Painlevé coordinates. I won't go into the details here because I've already discussed them in the question Why is a black hole black? I'll simply quote the result for the calculated velocity of an outgoing light ray as a function of distance $r$ from the singularity:

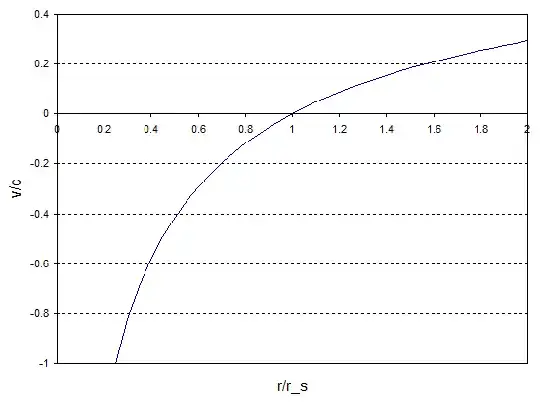
$$ \frac{v}{c} = 1-\sqrt{\frac{r_s}{r}} $$

And if we graph the velocity of light calculated using this equation we get:

At large $r$, far from the horizon, the velocity of the light is reduced, which means when it gets to us it is red shifted. However the velocity is still position so the light is still moving away from the black hole.

At the event horizon, when $r = r_s$, the velocity falls to zero so the light is frozen at the horizon, and this corresponds to the infinite red shift.

Inside the horizon, for $r \lt r_s$, the velocity becomes negative so even an outgoing ray of light is moving inwards towards the singularity. This would correspond to a greater than infinite red shift i.e. it has actually reversed the direction of the light.

But ...

This is all good fun, and the maths is fine, but the physical interpretation is highly suspect to say the least. The calculated velocity is not really a velocity in the sense we usually mean.