5

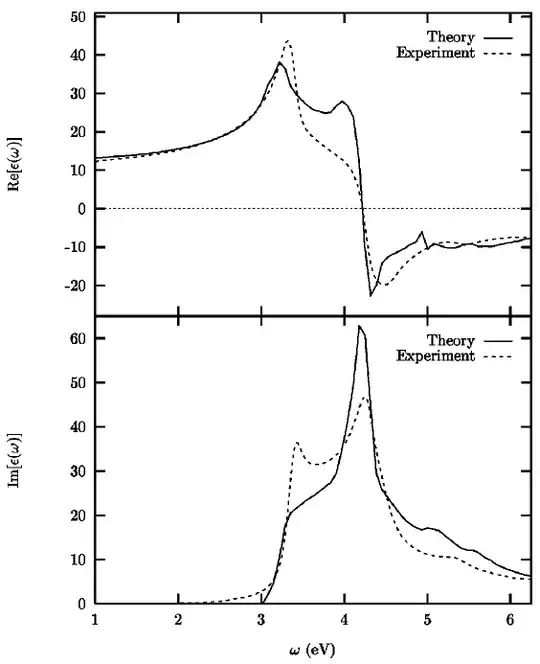
The dielectric functions of silicon from Phys. Rev. B 62, 7071

I basically understand the zero point of the real part of the dielectric function for a metal. It generally corresponds to plasmon. For a metal, if the frequency is lower, the real part is negative meaning that the light is completely reflected. The electrons around the surface can screen the electric fields of the light before it gets into the bulk. But if the frequency is higher than the plasmon frequency, the real part is positive and the metal behaves like a dielectric medium.

But I cannot get a physical understanding of the similar zero points for a semiconductor like silicon. Could anyone please help me on this?

Qmechanic
  • 220,844
John Cao
  • 51

2 Answers2

1

I would say that it corresponds to some kind of quasiparticle or in other words an elementary excitation of the system. The kind of excitation that can be responsible for the particular zero of $Re\left[\epsilon\right]$ you are looking it depends on what frequency it is at.

In the example you gave we have the zero approximately at $\omega \approx 4eV$. This corresponds to (now working with the light dispersion since that is what is getting absorbed): $\lambda \approx 3 \cdot 10^{-7}m$ which is in the ultraviolet. This is most likely still a plasmon of some kind, i.e. an oscillation of the electron gas (see also comment about semiconductor plasmons here).

Wolpertinger
  • 11,787
  • 4
  • 42
  • 94
1

Introduction: for metals, as you said, electrons can move to screen the fields. For low frequencies (less than the plasma frequency), the electrons are able to move fast enough to screen the fields; for high frequencies (greater than the plasma frequency), the electrons cannot move fast enough, and they do not "succeed" to screen the fields, which can penetrate the material.

Addressing your question: on the other hand, you can imagine a semiconductor as an ensemble of positive charges with bounded electrons around them. An electric field polarizes those charges: the positive charges are slightly displaced in one direction whereas the negative charges are pulled a little bit in the opposite. Neither of them can mover far away from their original position. However, in between of them and due to that polarization, the material has created an electric field opposing to the external field. There you have the physical mechanism by which the material moderately (or strongly, depending on its polarizability) changes or screens the applied fields. The frequency now plays the same role as in the case of metals, concerning the ability of the material to react "on time" to screen the applied fields.

Godoy
  • 116