1

I know that equivalent capacitance of multiple capacitors in series is $$ C = \left(\frac{1}{C_1} + \cdots + \frac{1}{C_n}\right)^{-1} $$ and in parallel is $$ C = C_1 + \cdots + C_n. $$ But there are circuits that are neither in parallel nor series. So what is the canonical definition of equivalent capacitance? This question sprung to mind when I tried to find equivalent capacitance in this circuit:

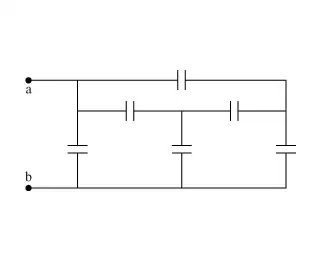
enter image description here

Apparently, there are some techniques known as Y-Delta transforms. But I wouldn't understand it without a clear definition of equivalent capacitance.

Myath
  • 121

3 Answers3

2

The definition of equivalent capacitance between two points $a$ and $b$ is as follows -- Insert a total charge $q$ through point $a$ and remove a total charge $q$ from point $b$. Then find the potential difference $V$ between the points $a$ and $b$. The equivalent capacitance between these two points is then defined as $C = \frac{q}{V}$. Note that if everything is done correctly here, $C$ should be independent of $q$.

For instance, let us use this definition to derive the series/parallel formula.

When the capacitances are in series, then all the capacitances have charge $q$ deposited on them. Then, the potential difference across each capacitor is $V_i = \frac{q}{C_i}$. The total potential difference across the series of capacitors is then $$ V = \sum_i V_i = q \sum_i \frac{1}{C_i} $$ Then, we have by definition of capacitance, $C = \frac{q}{V} \implies \frac{1}{C} = \frac{V}{q}$ and therefore $$ \frac{1}{C} = \sum_i \frac{1}{C_i} $$

When the capacitances are in parallel, the charges $q_i$ must be deposited so that $\sum q_i = q$ and that the potential difference across each capacitor is equal to $V$. Then, we have the formula $$ V = \frac{q_1}{C_1} = \frac{q_2}{C_2} = \cdots $$ Using this, we have $q_i = V C_i$. Summing over $i$, we have $$ q = \sum_i q_i = V \sum_i C_i \implies \frac{q}{V} = \sum_i C_i = C $$

Thus, we have used the general method above to derive the equivalent capacitances as required. For more complicated circuits (such as the one you have) you'll have to go back to the drawing board and use the general method I've described above.

Prahar
  • 29,157
1

A lot of problems of this type can be solved by rearranging the circuit into a more user friendly form.

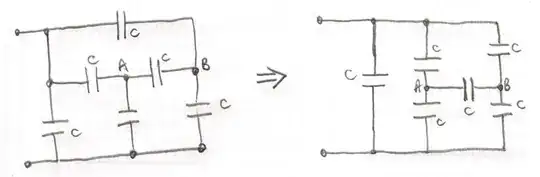
enter image description here

By symmetry you can say $V_{AB}=0$ and so you get $2C$ as the equivalent capacitance.

There is a method for solving such network problems which goes back to first principles and is equivalent the using Kirchhoff’s law which are based on the conservation of charge and the conservation of energy.

The first thing to do is draw the circuit and label it.
In this case I missed out the left hand capacitor because it will just be in parallel with the equivalent capacitance of the circuit which is left.

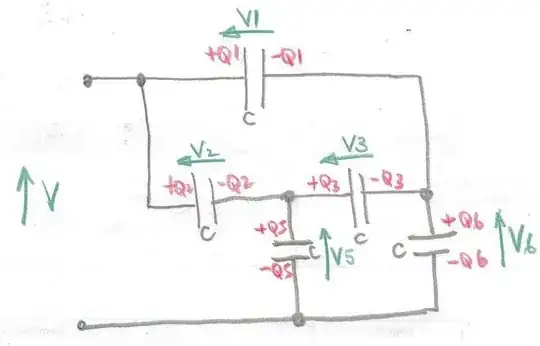
enter image description here

Label the charges $+Q_1, -Q_1$ on each of the capacitors and the voltages $V1$ with an arrow to indicate direction of increased potential.
Looking at the diagram the equivalent capacitance of the network will be $\frac{Q_1+Q_2}{V}$ so you need to find $Q_1+Q_2$ in terms of $V$ and $C$.
For each capacitor there is a relationship of the form $Q_1=CV_1$.

Looking at the charges first noting that the total charge at each node where only capacitors are connected must be zero.

$-Q_2+Q_3+Q_5 = 0$ and $Q_3-Q_1+Q_6 = 0$

Adding these two equations together $\Rightarrow Q_1+Q_2-Q_5-Q_6= 0 \Rightarrow V_1+V_2=V_5+V_6$

Now looking at the voltages:

$V=V_1+V_6$ and $V= V_2+V_5$

Adding these two equations together

$\Rightarrow 2V =V_1+V_2+V_5+V_6 \Rightarrow 2(V_1+V2) \Rightarrow \dfrac {2(Q_1+Q_2)}{C}$

So the equivalent capacitance is $\dfrac{Q_1+Q_2}{V} = \dfrac{CV}{V} = C$

For the whole circuit the equivalent capacitance is $2C$.

Farcher
  • 104,498
-1

,hi we know Q=CV so dQ=Cdv dQ/dv=C

a short way that you talked triangle-star formulation for calculation it,

but in really we consider q like a flow of current,voltage like former voltage( vs a resistor),here we have capacitor instead a resistor. for calculation equivalent capacitance ,we insert a charge source (same current source ) and we use Node equation or Mesh equation (they are in engineer electronic book i.e. my books ) and we write the equation and we try to get the
ratio Q/V.

this ratio is called equivalent capacitance( of top circuit).

stackprogramer
  • 189