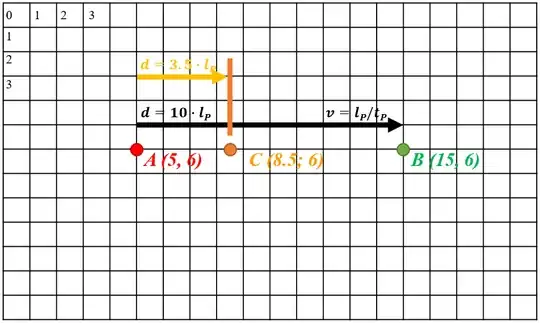
Consider a photon, positioned in space in a finite portion of a grid. Any point of the grid is vertically or horizontally aligned, each distanced by a Planck unit.
$l_P = 1.616 199(97) × 10−35 m$
The speed of the photon is, in this grid, $v = l_P/t_P$
The photon is first captured at its original point $A$, when $t = 0*t_P$ and $x_A = 5*l_P$.
It is then captured at point $B$, when $t = 10*t_P$. Logically, the position of point B is $x_B = x_A + 10*l_P = 15*l_P$, and $y_B = y_A$.
This is a two-dimensional representation of the aforementioned grid:
The problem here is the actual definition of the Planck distance unit. By definition, a Planck distance can only have a natural coefficient, which means that the unit cannot have a fractional-represented coefficient with it.
Mathematically, it is possible to divide any unit in half. However, the Planck time unit is calculated using the Planck distance unit as well, which means it cannot be fractional as well.
Since the definition of Planck units describes how they cannot be fractionally split, the photon is never going through the $3.5 * l_P$ mark during its movement. Does that mean that we can define time as a frame cycle, where the fastest frame rate is $1*t_P$, and that the photon basically changes position to the closest Planck distance grid point (without having a transitional point in space and time during the process)? In other words, does the photon even reach point $C$ during the translation from $A$ to $B$?