Estimates of the amount of for example "dark matter" are of interest to the cosmologists. However, I have never seen an estimate of how many "free" photons could be speeding about in the known universe on average at any one time. I don't even know if the question has any meaning but I would presume a summation of the total energy radiated per second in all directions from all stars in all galaxies would provide a first indication of the magnitude in question. Could their combined energy somehow be a part of the so-called "dark energy"?
2 Answers
Photon number density
The number density of photons in the Universe is roughly 410 per cm$^3$ (a tad larger than the approximation in the source given in the comments, which uses the average photon energy), and is dominated by the Cosmic Microwave Background (CMB) radiation. Photons from stars/galaxies are more than two orders of magnitudes smaller in number, and may thus be neglected. This answer provides a graphical overview of the various contributions.
Total number of photonsIf you're interested in the total number of photons in the (observable) Universe, multiply by its volume given by its radius of 47 billion lightyears (you cannot calculate its radius as you do in your comment, because the expansion rate is unrelated to the speed of light) to get roughly $10^{89}$ photons. This number is roughly constant throughout the history of the Universe (but the energy isn't).
Relation to dark energyThe energy of photons contributes to the total energy of the Universe, but decreases with the expansion to the fourth power, as discussed in Evan Rule's answer. This energy is "normal" energy, however, in the sense that it results in a gravitational force (which today is negligible, but dominated until the Universe was ~47,000 years old), and thus acts so as to decrease the rate of expansion. In contrast, dark energy has the opposite effect of increasing the rate of expansion. So the answer to your last question is no.
Relation to dark matterIn principle, radiation or radiation-like particles such as neutrinos, could be at least a part of dark matter. This would be so-called "hot dark matter", but its significance has been ruled out as a major contributor, as it would wash out cosmological structures rather than cause them (see e.g. this question + answers).
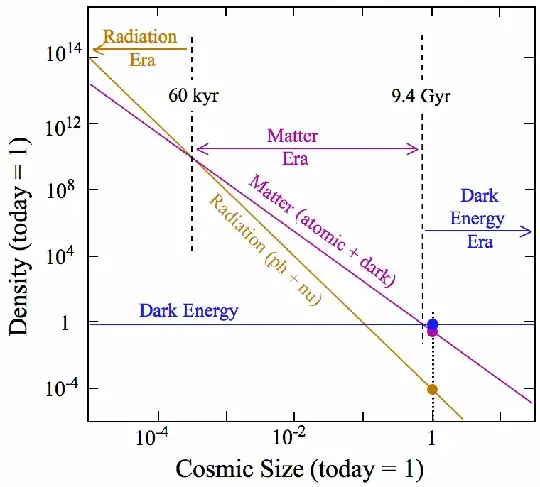
Photon energy density does affect the expansion of the universe, similar to the effect of dark matter and dark energy. At the present time, however, the photon energy density has a much smaller effect than either dark energy or dark matter. This is due to the different ways in which the energy densities of the various components scale with the size of the universe. Dark matter energy density (unsurprisingly) scales like ordinary matter density \begin{equation} \rho_{DM}\propto a(t)^{-3}. \end{equation} That is, as the universe expands and the scale factor increases, the dark matter energy density decreases by three factors of scale, one for each spatial dimension.
Photons, however, in addition to having their density diluted by the expansion of space, are also redshifted, so that their energy density drops by an additional inverse scale factor \begin{equation} \rho_{\gamma}\propto a(t)^{-4}. \end{equation} Lastly, we have dark energy, also referred to as the cosmological constant. It is constant with respect to scale factor.
So, we see that as time evolves and the scale factor increases, dark energy density is constant, dark matter density drops as $a(t)^{-3}$ and photon energy density drops like $a^{-4}$. This is the reason why we currently live in a period of accelerating expansion: radiation and dark matter density have been sufficiently diluted by expansion so that dark energy dominates.
It is important to note that the universe evolves differently during periods dominated by either radiation, dark matter or dark energy. Specifically, only dark energy can produce accelerated expansion. Radiation and dark matter both act to slow and eventually reverse expansion, albeit in quantitatively different manners.
At sufficiently early times, when $a(t)\ll 1$, the photon density will be large compared to the dark matter density and dark energy density. During this radiation-dominated epoch, radiation energy density will drive scale factor evolution.
The graph below shows how the scale factor evolved in a universe like our own. Following an initial period of exponential expansion (inflation), the universe was radiation dominated, then matter-dominated, and finally dark energy-dominated.
Finally, a calculation of the present day photon energy density from the CMB temperature can be found in this answer.