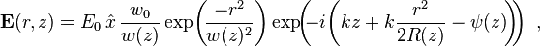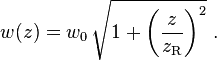Why does a laser beam stay collimated?

Question

I am looking for a simple way of explaining the collimation of a laser beam. The typical discussion of the two slit experiment of quantum theory relies heavily on the Huygens principle. Its application to a laser beam would tend to predict spreading. From a purely electromagnetic field point of view, how can one visualize what happens at the edge of the beam?

Answer 1

Just as Jon Custer wrote in his comment, even a perfectly collimated laser beam with a planar wavefront will diverge. The way it happens is determined by the Huygens principle, and depends on the beam profile:

When the light intensity is abruptly cut by a sharp flat obstacle, the light will indeed diffract in almost all angles. A razor blade cutting a laser beam, even though viewed from the geometric shadow, will still have a bright rim. (In wave optics, no absolute shadows exist!)

When the intensity of the beam is modulated smoothly, it will diffract in small angles only. Intuitively it can be imagined that at the edge of a beam passing through a "soft aperture", the Huygens elementary source with slightly higher amplitude than its neighbour forces the resulting wavefront to be bent away by a minute angle, outwards from the beam axis. It is still all about the superposition of spherical waves.

Edit: To illustrate this, I employed my open-source simulation scripts, using the excellent MEEP Maxwell-equations solver, to a classical edge-diffraction experiment. In the following three animations, I computed for you a wave diffraction on a sharp edge (left), and on "soft apertures" with characteristic transition width of 50 % and 100 % of the full image width.

Answer 2

A properly collimated laser beam is called a Gaussian Beam whose transverse magnetic and electric field amplitude profiles are given by the Gaussian function.

The Gaussian beam is a transverse electromagnetic (TEM) mode. The mathematical expression for the electric field amplitude is a solution to the paraxial Helmholtz equation:

The width of such laser beam is described by:

The relationship between beam width and divergence is a fundamental characteristic of diffraction, and of the Fourier transform which describes Fraunhofer diffraction.

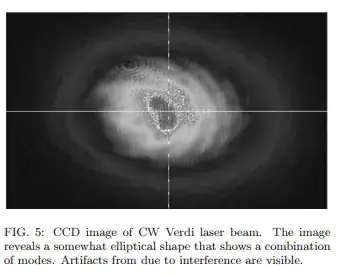
Here is how a Gaussian beam¹ looks:

---

^{1. Excerpt from the following article: Quantitative and Qualitative Study of Gaussian Beam Visualization Techniques}