1

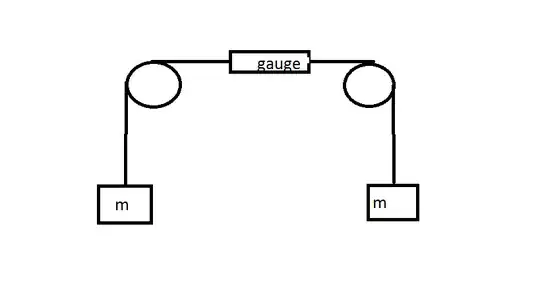
There is a system composed a rope connecting two identical masses, each of mass $m$, suspended by two fixed pulleys. The system is in a static equilibrium.

In between the pulleys, there is a tension gauge in the rope. It is my understanding that this tension gauge should read $mg$, as it is being pulled on both ends with a force of $mg$, exactly the same as if it were simply suspended from a fixed point holding a mass of $m$.

However, my professor says the tension gauge reads $\frac{mg}{2}$. What is correct, and why? enter image description here

Vinay5forPrime
  • 423
  • 3
  • 11
Jackson
  • 121

3 Answers3

3

You should go and find another professor.

For the left hand mass because it is in equilibrium T-mg=0 and there is a similar equation for the right hand mass. For the gauge T-T=0. So the gauge is reading the value of T.

Farcher
  • 104,498
1

The professor is wrong (for how you labeled the diagram). The answer is $mg$. But if he meant $m_{total} g / 2$ he was correct. That is $(m_1+m_2) g / 2$ is the correct answer.

Curt Welch
  • 111
0

In fact, the tension within the gauge should me mg because of how there are 2 masses on two pulleys.

Resolving upwards on the left pulley, and that the system is in static equilibrium, T - mg = 0 therefore T = mg.

Same with the other pulley, resulting into two tensions occurring at both sides. Now that one tension occurs to the left of the gauge and one to the right, this means that total tension is T (because T - T = 0). Since T = mg, tension in gauge is mg.

SergeantSerk
  • 291