Consider the following experiment:
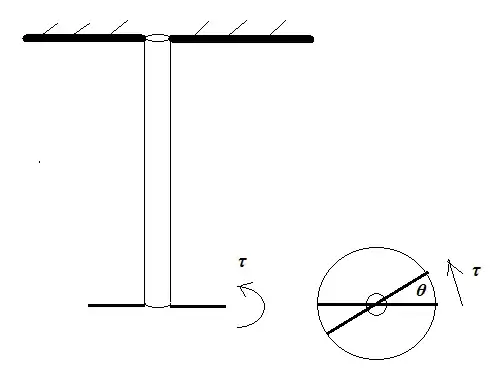
A regularly shaped metal rod is fixed at its top to a ceiling (or such like), so it cannot move. At the bottom of the rod we rigidly attach two strong and heavy handle bars, which allow to exert a torque $\tau$ to the rod.
As a result of this torque the rod now torsionally deforms, so that the handle bars are now at an angle $\theta$ with regards to their initial position. As long as the deformation is elastic (and not plastic, that is: for small $\theta$) we can write:
$$\tau = k \theta$$
where $k$ is the torsional spring constant of the rod.
What happens when we suddenly remove the torque $\tau$? The rod and handle bars will enter into a simple harmonic oscillation, as follows.
For simplicity's sake we'll assume the rod to be massless and the inertial moment of the handle bars (with respect to the rod's central axis) to be $I$, then with Newton's Second Law (applied to rotation) we can write the equation of motion of the handle bars as:
$$I\frac{d^2\theta}{dt^2}=-k\theta$$
Which has the well-known solution:
$$\large{\theta=\theta_0 \cos \omega t}$$
with $\theta_0$ the angle at $t=0$ and:
$$\omega=\sqrt{\frac{k}{I}}$$
and $\omega=2\pi f$ where $f$ is the frequency of oscillation. Note for example that for a stiffer rod (higher $k$) the frequency is higher.
The same question applies to bending vibration
Remove the handle bars and replace the torque with a force acting on the end of the rod and perpendicular to it. Elastic deformation now causes the rod to bend. On sudden release something analogous to the above case happens. The rod will also enter into a simple harmonic (bending) oscillation with frequency derived from the equation of motion and the system's parameters (mass and stiffness). A real-life example is that of a tuning fork: when struck by the hammer it produces a pure pitch sine and by transmitting its oscillation to air, audible sound waves are formed.
